티스토리 뷰
기계학습이 다루는 데이터는 주로 '불확실성'을 가지고있는 실생활로부터 온 데이터들, 따라서 자연스럽게 기계학습 역시 확률과 통계를 잘 활용해야만 좋은 모델을 만들 수 있다.
1. 확률 기초
확률변수와 확률 분포
도,개,걸,윷,모가 나오는 윷놀이가 있다.
먼저 확률을 수식으로 표현하려면 위 다섯가지 경우의 수들 중 한가지를 나타내는 변수가 필요하다. 이렇게 어떤 상황이 발생하는지를 나타내는 변수를 확률변수(random variable)이라고 하며 주로 영어 소문자로 나타낸다.
그리고, 윷놀이에서는 이런 확률변수가 각각 [도, 개 ,걸, 윷, 모]로 5가지가 존재하며 이 확률 변수 전체의 모임을 '정의역'이라 부르며 보통 영어 대문자로 나타낸다..
전체 정의역에 걸쳐 확률값을 모두 표기한 것을 확률 분포(probability distribution)이라고 한다.
보통 확률분포는 P(x=도) 또는 P(도)와 같은 형태로 나타낸다. 또는 확률변수 x들은 정의역 X의 분포를 따른다는 의미를 강조하기 위해서 다음과 같이 나타내기도 한다. PX(x=도)
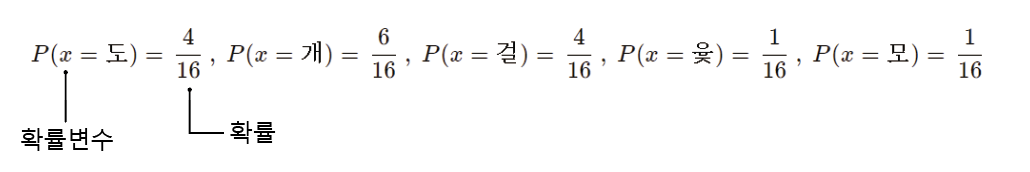
확률 분포는 그래프로 나타낼 수도 있다. 이때 정의역이 중요한 역할을 하는데, 정의역의 갯수가 유한하면 이산형확률분포로써 '확률질량함수(probability mass function=PMF)'라고 이야기하며 정의역 갯수가 무한하여 셀수없다면 연속형확률분포로써 '확률밀도함수(probability density function=PDF)'라고 이야기한다.
윷놀이는 정의역이 5개로 유한하기때문에 확률 질량함수를 그릴 수 있다.

확률 질량함수가 마치 히스토그램처럼 막대형태로 뚜렷이 구분되는 반면 보통 확률 밀도함수는 다음과 같이 나타내어진다.
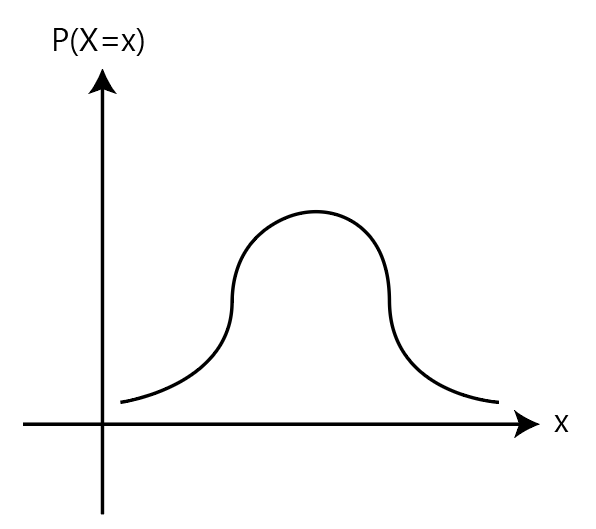
공통점은 확률 질량 함수나 확률 밀도함수 둘 다 정의역에 속하는 모든 확률변수의 확률값을 더했을 때는 반드시 1이 되어야 한다는 것인데, 다시말하면 PMF나 PDF모두 그래프 아래의 면적은 반드시 1이 되어야한다는 점이다.
곱 규칙과 전확률 규칙(Law of total probability)
곱 규칙과 전확률 규칙을 알아보기 전에 먼저 조건부 확률과 결합확률에 대한 개념을 확실히 이해하자.
조건부 확률(Conditional probability)과 결합확률(Joint probability)는 상당히 헷갈리기 쉬운 개념인데 두 확률의 차이를 명확히 구분짓지 못한다면 생성모델 등 확률분포에 기반하는 모델을 이해할 때 상당히 괴로울 것이다.
우리가 중고등학교때 계속 배워왔던 교집합의 개념, 즉 'A 사건과 B 사건이 동시에 발생할 확률'이 결합확률이고 조건부확률은 'A 사건이 발생하였음을 알았을때, B 사건이 발생할 확률'을 이야기한다.
결합확률은 사건 A와 B의 분포를 따르는 확률분포의 의미를 강조하기 위해 PA,B(A=a, B=b)처럼 표기하거나 그냥 P(a,b)로 표기하며 간혹 P(ab)처럼 표기하기도 한다. 본인은 표기하는 사람들 마다 서로 다른 확률분포 표기방식 때문에 한참을 헤메였는데(지금도 그렇다) 방금 표기한 모든 방식들의 의미는 결국 우리가 중고등학교에서 배운 P(a ∩ b)의 의미와 똑같은 의미이다.
조건부 확률은 사건 A가 이미 발생했다는 전제 하에, 사건 B가 발생할 확률이라는 의미로 P(B|A)로 표기한다.
결합확률과 조건부 확률의 관계를 나타내는 규칙이 바로 곱 규칙이다.
P(A, B) = P(A ∩ B) = P(AB) = P(A|B)P(B)
이때 P(A ∩ B) = P(B ∩ A) 임은 자명하므로
P(B, A) = P(B ∩ A) = P(BA) = P(B|A)P(A)
따라서 P(A, B) = P(A|B)P(B) = P(B|A)P(A) = P(B, A)
조건부 확률에 대해서 좀 더 자세하게 다룬 포스팅도 있으니 혹시 궁금한 사람이 있으면 참고해보면 좋을듯하다.
https://biomadscientist.tistory.com/20
조건부 확률 (Conditional probability)
해당 내용은 김성범교수님의 유튜브 강의 내용을 정리한 것입니다. 개인 공부를 위함이고 잘못된 내용이 있을 수 있으니 참고만 하시길 바랍니다. https://www.youtube.com/watch?v=Cj25K_leYZw&list=PLpIPLT0Pf7I
biomadscientist.tistory.com
돌아와서, 글로만 읽어서는 이해가 어려울 수 있으니 아주 간단한 예시를 하나 들어보자.

P(Black|세모)는 조건부 확률로써 "상자에서 도형 하나를 뽑았는데 세모였음을 알게되었다, 이때 검은색일 확률은?"이며
P(Black, 세모)는 결합확률로써 "상자에서 도형 하나를 뽑았는데 검은색 세모일 확률은?"이다.
미묘하게 다르지만 분명하고 엄격하게 서로 다른 의미이며, 서로를 반드시 구분할 수 있어야한다.
어쨌든, 곱 규칙에 의해 P(A,B) = P(A|B)P(B) = P(B|A)P(B) = P(B,A) 이므로 이 식을 이용하면 다음과 같다.
$$P(black| \triangle) = \frac{P(black \cap \triangle)}{P(\triangle)} = \frac{\frac{2}{7}}{\frac{3}{7}} = \frac{2}{3}$$
$$P(black,\triangle) = P(black|\triangle)P(\triangle)= \frac{2}{3} *\frac{3}{7} = \frac{2}{7}$$
전확률의 법칙을 이해하기 위해서 먼저 다음과 같은 그림을 보자

전확률 규칙은 다음처럼 어떤 표본공간 S가 각각이 서로에게 배반인 사건들로 나누어져 있음을 가정하에, 이 사건들에 걸쳐 존재하는 어떤 사건의 전체 확률을 구할때 사용한다.
위에서 전체 불량률을 구하기 위해서는 다음과 같은 전확률 규칙에 의해 구하면 된다.
$$P(불량률) = \sum_{i=1}^kP(불량률 \cap공정_i)=\sum_{i=1}^kP(불량률|공정_i)P( 공정_i)$$
전확률 규칙은 글로 설명하기 어려운 부분이 있어서 잘 설명된 동영상로 대체한다.
https://www.youtube.com/watch?v=4zptP2UNdCE
https://youtu.be/Cj25K_leYZw?list=PLpIPLT0Pf7IqS4as3nefPyGv94r2aY6IT&t=1150
'Background > Math' 카테고리의 다른 글
| CNN에서 pooling과 global pooling의 차이는 무엇인가? (0) | 2023.04.16 |
|---|---|
| [오일석 기계학습] 2.2 수학 - 확률과 통계 - 베이즈 정리 (0) | 2023.04.12 |
| [오일석 기계학습] 2.1 수학 - 선형대수(2) (0) | 2023.03.31 |
| [오일석 기계학습] 2.1 수학 - 선형대수(1) (0) | 2023.03.29 |
| 1x1 Convolution은 무엇을 위해서 하는가? (0) | 2023.03.14 |
- Total
- Today
- Yesterday
- marginal likelihood
- 3b1b
- 나노바디
- 선형대수
- manim library
- 이왜안
- 파이썬
- manim
- 최대우도추정
- 3B1B따라잡기
- dataloader
- 오일석기계학습
- Manimlibrary
- Matrix algebra
- MorganCircularfingerprint
- elementry matrix
- 베이즈정리
- antigen antibody interaction prediction
- ai신약개발
- 논문리뷰
- 기계학습
- nanobody
- 인공지능
- 백준
- MLE
- eigenvalue
- 항원항체결합예측모델
- eigenvector
- MatrixAlgebra
- manimtutorial
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
