티스토리 뷰
기계학습에서 널리 사용되는 분포로는 가우시안분포와 베르누이분포, 이항분포가 있다. 이 분포들은 1개 또는 2개의 매개변수로 분포 형태를 쉽게 조절할 수 있다.
가우시안 분포(Gaussian distribution)
가우시안 분포는 평균(μ)과 분산(σ2)을 나타내는 2개의 매개변수로 분포 형태가 정해진다. 가우시안 분포 중 평균이 0 분산이 1인 분포를 특히 정규분포(normal distribution)라고 한다. 가우시안 분포는 N(x; μ, σ2)또는 N(μ, σ2)으로 나타낸다. 세미콜론 앞에는 확률변수를, 세미콜론 뒤에는 분포를 나타내는 매개변수를 나타낸다. 자연적으로 발생하는 현상들은 주로 가우시안 분포와 유사한 형태를 나타낸다. 예를들어 사람의 키, 영상에 나타나는 잡음 신호, 성적 등이 대표적인 가우시안 분포를 따르는 현상들이다.

위 식은 성적이나 사람의 키 분포처럼 오직 하나의 확률변수로 나타내어지는 분포를 나타내는 식이다. 그러나 기계학습에서 실제로 분포를 나타내는 데이터가 가지는 확률변수는 최소 2개에서 많게는 수만개까지도 가능하다. 이렇게 특징 벡터가 1차원 이상인 d차원의 벡터일때 가우시안 분포는 평균 벡터(μ)와 공분산행렬(∑)로 나타낸다. 이때 식은 다음과 같다.
예를들어 물고기를 전체 길이, 꼬리의 길이, 지느러미의 갯수를 이용해 나타냈다면 여기서의 특징 벡터는 3차원이 된다.
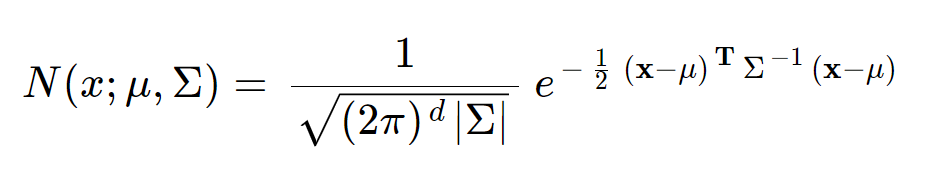
|∑|값은 공분산행렬 ∑의 행렬식 det(∑)이다. 그리고 지수함수의 지수는 마할라노비스 거리라는 개념인데 이에 대한 개념으로는 다음 사이트를 참고하면 좋을 것 같다.

https://angeloyeo.github.io/2022/09/28/Mahalanobis_distance.html
마할라노비스 거리 - 공돌이의 수학정리노트
angeloyeo.github.io
베르누이 분포와 이항 분포
확률변수 x가 1(성공) 또는 0(실패) 두 가지 값만 가질 수 있는 이진변수이며, 성공 확률은 p, 실패확률은 1-p인 분포를 베르누이 분포라고 한다. 이해가 안간다면 동전던지기를 생각하면 된다. 동전던지기는 대표적인 베르누이 분포를 따르는 현상이며 성공과 실패확률은 0.5로 동일한 경우이다. 베르누이 분포는 다음과 같이 나타낸다.
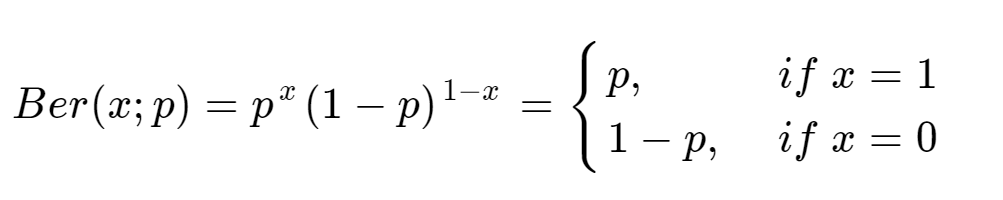
그리고, 성공확률이 p인 베르누이 실험을 m번 수행할 때 성공하는 횟수의 확률 분포를 이항분포(Binomial distribution)이라고 한다. 매개변수는 p와 m이다. 이항분포도 어렵게 생각하지 말자. 동전던지기 그대로 이용하면 된다. 동전을 10번 던졌을때 앞면이 0번 나올 확률, 1번 나올확률 ... m번 나올 확률을 나타내는 분포를 생각해보면 된다. 이때 동전던지기는 앞면이 나올 확률이 0.5이므로 B(x; m, p=0.5)으로 나타낼 수있다. 이항분포는 다음과 같이 나타낸다.

'Background > Math' 카테고리의 다른 글
| 선형대수학 Linear Algebra 용어 및 기초 이론 정리/모음 (0) | 2023.05.25 |
|---|---|
| [오일석 기계학습] 10.4 - 확률 그래피컬 모델 RBM과 DBN (3) (0) | 2023.05.06 |
| [오일석 기계학습] 10.4 - 확률 그래피컬 모델 RBM과 DBN (2) (0) | 2023.04.27 |
| [오일석 기계학습] 10.4 - 확률 그래피컬 모델 RBM과 DBN (1) (0) | 2023.04.26 |
| [오일석 기계학습] 2.2 수학 - 확률과 통계 - 최대우도법 (0) | 2023.04.26 |
- Total
- Today
- Yesterday
- MorganCircularfingerprint
- ai신약개발
- 오일석기계학습
- Matrix algebra
- elementry matrix
- manimtutorial
- nanobody
- manim
- MatrixAlgebra
- 최대우도추정
- Manimlibrary
- 3B1B따라잡기
- antigen antibody interaction prediction
- 항원항체결합예측모델
- MLE
- 논문리뷰
- marginal likelihood
- 파이썬
- 백준
- 인공지능
- manim library
- 이왜안
- dataloader
- 3b1b
- 베이즈정리
- eigenvalue
- 선형대수
- 나노바디
- eigenvector
- 기계학습
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
