Geometric distribution/ Pascal distribution

내용의 출처는 인프런 - 조범희님의 확률과 통계 기초 강의입니다.

 

1. Geometric distribution (PX(x)) [X ~ Geometric(p)]

 

: 불공평한 동전을 던진다. 이 때 앞면이 나올 확률 P(H) = p, 뒷면이 나올 확률을 P(T) = 1-p 라고 하자. 

이때의 Random Variable X = 처음으로 앞면이 나올때까지 던진 coin tosses횟수이다. 즉 X = {1, 2, 3, ...}이다.

 

X = 1 일때 P_X(1) = p = (1-p)⁰p

X = 2 일때 P_X(2) = (1-p)p = (1-p)¹p

X = 3 일때 P_X(3) = (1-p)(1-p)p = (1-p)²p

 

X = n 일때 P_X(n) = (1-p)(1-p)...(1-p)p = (1-p)^n-1p

 

따라서 Geometric distribution의 PMF는 P_X(n) = (1-p)^n-1p이다. where, n = 1, 2, ...

파라미터 p에 따른 Geometric distribution의 분포

 

Geometric distribution의 RandomVariable X를 처음으로 앞면이 나오기까지 총 실패횟수로 두어도 Geometric distribution을 따른다.

 

---

 

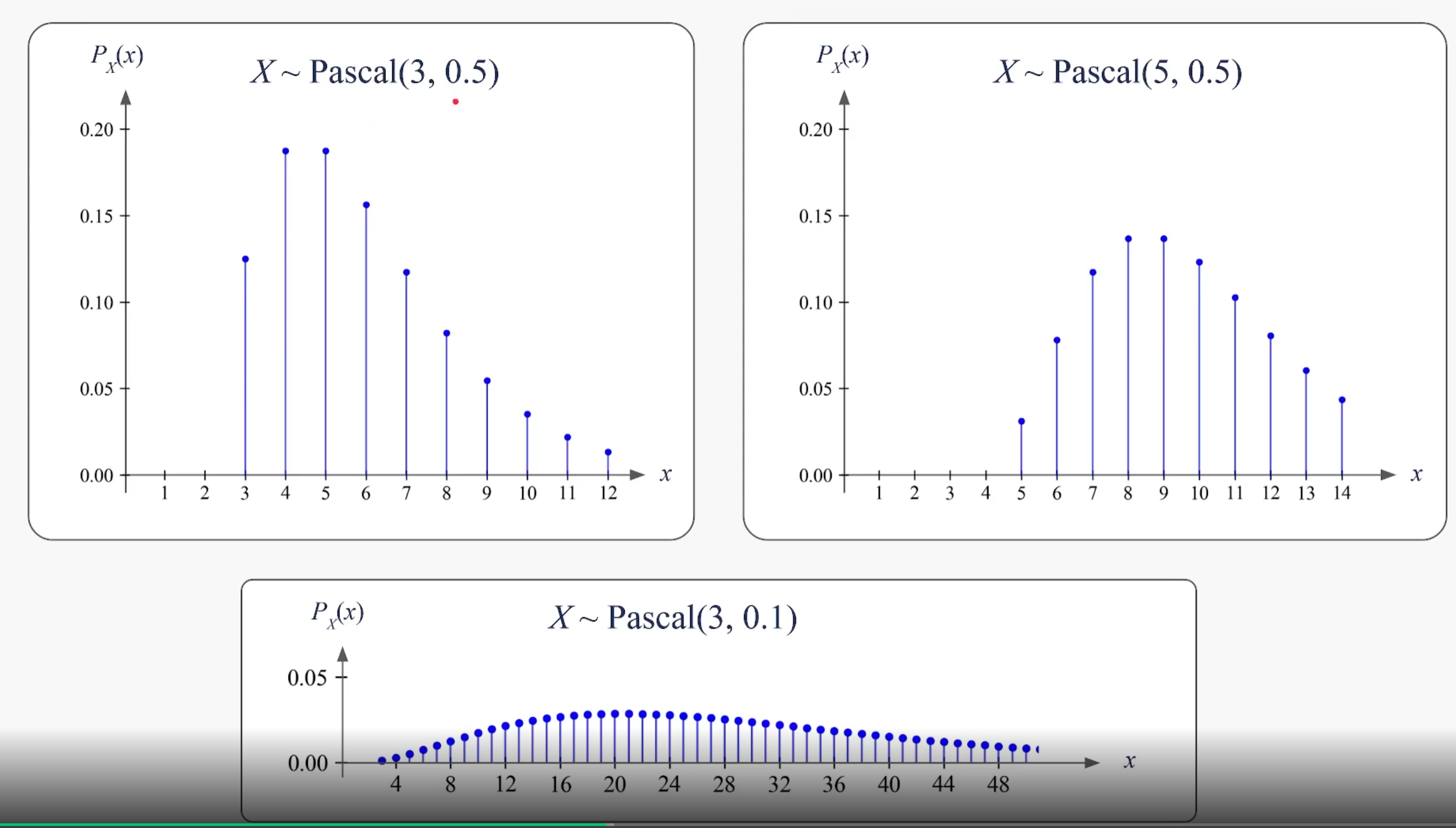
2. Pascal distribution (PX(x)) [X ~ Pascal(m, p)]

 

: 불공평한 동전을 던진다. 이 때 앞면이 나올 확률 P(H) = p, 뒷면이 나올 확률 P(T) = 1-p이다.

이때의 RandomVariable X = 총 m번의 앞면이 나올 때 까지 던진 coin tosses횟수이다. 즉 X = {m, m+1, m+2, ...}

m이라는 파라미터가 추가되었음에 주의하자.

 

예를 들어, 총 2번의 앞면이 나올 때 까지의 Pascal distribution은 X ~ Pascal(2, p)

P_X(i)로 나타내자.

X = 2 일때 P_X(2) = pp = {HH}

X = 3 일때 P_X(3) = (1-p)pp 또는 p(1-p)p {THH, HTH}

X = 4 일때 P_X(4) = (1-p)(1-p)pp 또는 (1-p)p(1-p)p 또는 p(1-p)(1-p)p {TTHH, THTH, HTTH}

...

 

이 때 우리는 Pascal distribution을 2개의 intersection으로 나눠서 생각해 볼 것이다.

바로 이렇게

 

위에서 언급한 Pascal Distribution X ~ Pascal(2, p)를 Event A라고 하자 A는 i번째에 m번의 앞면을 볼 때 까지 동전을 던진 횟수가 된다. 이때 intersection으로 나눠서 생각해보면 다음과 같다.

Event B = i - 1번을 던져서 m - 1번의 앞면을 볼 사건

Event C = 1번을 던져서 1번의 앞면을 볼 사건

이때 Event A는 B 사건 이후에 C 사건이 발생할 확률이므로 P(A) = P(B, C) = P(B ∩ C)이다. 그리고 이때 사건 B와 사건 C는 당연히 독립(independent)이므로 P(A) = P(B)P(C)이다.

Event B와 C는 Binomial Distribution, Bernoulli distribtuion임을 알 수 있다. 따라서 B와 C의 확률은 다음과 같다.

따라서 Event A의 발생 확률 P(A) = P(B)P(C)로부터 다음과 같다.

따라서 Pascal(m, p)의 PMF P_X(i) = _i-1C_m-1p^m(1-p)^i-m이다. 

 

이때 m = 1이라고 생각해보자.

조합(C)에서 0개를 뽑는 경우의 수는 항상 1개뿐이라 1이다.

 

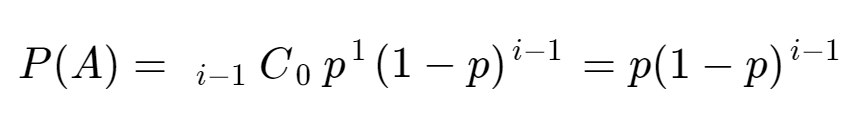
Geometric distribution과 완전히 동일한 것을 볼 수 있다. 즉 Geometric distribution은 Pascal distribution에서 m = 1인 경우와 완전히 동일한 distribution을 갖는다.

따라서Geometric(p) = Pascal(1, p)이다.

Pascal distribution