티스토리 뷰
Banach's fixed point theorem/contraction mapping theorem 바나흐 고정점 정리
벼랑끝과학자 2024. 1. 30. 22:09https://www.youtube.com/watch?app=desktop&v=9jL8iHw0ans
https://lykelee.github.io/banach-fixed-point-theorem/
출처는 언제나 그렇듯, 인?도 형이다.
나는 수학 전공자가 아니기 때문에 엄밀히 따진 수학적 의미로는 틀린 표현을 많이 사용할 수 있고, 공부하며 적는 내용이기 때문에 잘못된 설명이 있을 수 있다. 포스팅은 참고만 하자.
Fixed Point
먼저 Fixed point(고정점)이라는 개념부터 배우자면, 단순한 fixed point의 개념은 매우 간단하다. 그냥 어떤 함수 f(x)에 대해서 f(x)=x 의 해가 되는 point를 고정점이라 한다. 기하학적으로는 고정점의 x값을 함수 f에 input하여도 x값이 변하지 않는 point를 의미한다. 예를들어 f(x) = 2x-1이라고 하자, x=1을 넣어보면 f(1) = 1로 input x의 값도 1이고 f(x)의 값도 1이다. 또는 f(x)=4x는 어떤가? 4x = x 의 해를 구하면 되므로 고정점은 0이다. 반면 f(x)=x+1은 x+1=x라는 방정식이 되어 1=0이라는 해가 없는 방정식이 만들어지기 때문에 고정점이 존재하지 않는다.
이렇게 단순한 의미의 고정점 개념은 임의 함수 f(x)=x인 해를 찾으면 된다.
Contraction Mapping Function T
바나흐 고정점 정리를 이해하기 위해서는 먼저 contraction mapping function에 대한 이해가 있어야 한다.
위키 찾아보면 거리공간이니 축약 사상 정리니 무슨말인지 모르겠다. 다 제끼고 나처럼 수학적 지식이 부족한 사람은 그냥 1차원 실수공간 R과 유클리디안 distance를 생각하자.
이제 임의의 함수 T : R → R을 생각하자. 이때 함수 T는 임의의 점 x와 y에 대해 다음의 성질을 만족하는 함수여야 한다.
- T(x)와 T(y)의 거리는 x와 y의 거리보다 반드시 짧아야 한다.

이런 함수를 Contraction mapping function이라고 한다.
아래 그림을 보자, ①또는 ②중 어떤것이 위 조건을 만족하는 contraction mapping function인가? 당연히 빨간 점으로 나타내진 ①만 함수의 결과 값 사이의 거리가 기존의 x,y보다 짧기 때문에 ①만 contraction mapping function이고 ②는 contraction mapping function이 아니다.
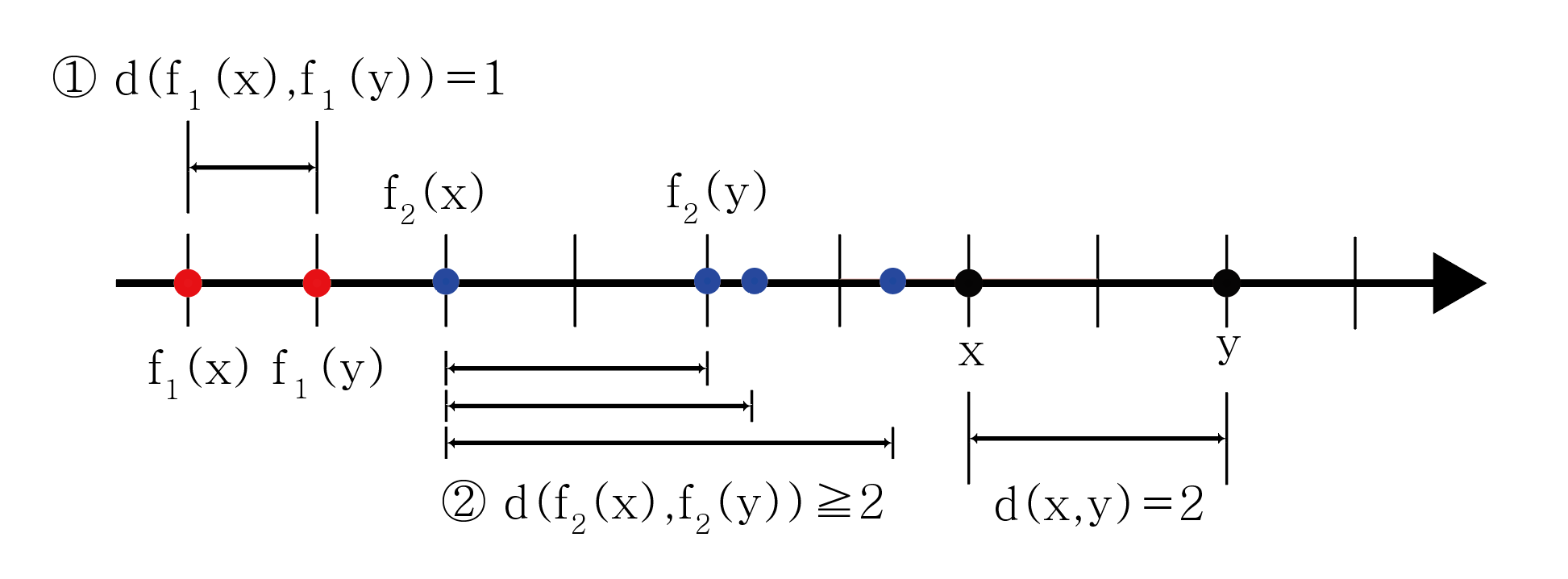
여기까지의 내용을 수식으로 나타내면 다음과 같다.

여기서 q ∈ [0,1)은 위에서 언급한 'T(x)와 T(y)의 거리는 x와 y의 거리보다 반드시 짧아야 한다'를 나타내기 위한 상수이다. 1이 포함되면 안된다는 것을 유의하자, 다시말해 그림2에서 파란 점들로 이뤄진 ②함수 값 중에 그나마 가장 짧은 경우도 d(f2(x), f2(y)) = 2 이므로 d(x,y)와 같기 때문에 최소한 q는 1과 같아야 한다. 이러면 q의 범위를 만족하지 못하므로 ②함수의 경우는 contraction mapping function이 될 수 없다는 것이다. 물론 2보다도 큰 그 외의 값들은 애초에 쳐다볼 필요도 없다.
Banach fixed point theorem
여기까지 이해했으면 Banach fixed point theorem을 설명할 준비가 되었다. 정의를 살펴보자.

거리공간 X (그냥 실수 공간으로 생각하면 된다고 하였다.)와 거리를 계산하는 함수 d가 있다. 이 공간은 non-empty complete metric space이고 Contraction mapping function T가 존재할때 T(x*) = x*를 만족하는 유일한 fixed-point x*가 존재한다.(uniqueness를 증명할 수 있기 때문에 공학수학에서 매우 유용하게 사용된다고 한다.) 그리고 x*는 다음식과 같이 함수의 mapping을 반복적으로 수행하여 찾을 수 있다. (start with 이하 구문인데 이 부분은 예시를 통해 쉽게 이해할 수 있으니 예시의 동영상을 꼭 확인해보자)
- non-empty complete metric space는 아래 포스팅을 참고
- https://biomadscientist.tistory.com/139

예시) start with 이하 구문이 무엇을 의미하느냐? 쉽게 생각하면 약간 이런느낌이다. 어떤 값을 넣고 계산기의 엔터를 마구마구 눌렀을 때 어떤 하나의 값으로 점점 수렴하는 것을 본 기억이 있는가? 다음 동영상을 한번 재생해보자.
9를 선택하던지, 6을 선택하던지, 7543을 선택하던지에 관계 없이(arbitrary element, 임의의 원소) Contraction mapping function의 결과값을 똑같은 함수의 입력값으로 무한정 반복하여 사용하는 경우라면 그 반복을 무한히 진행하였을 때 수렴하는 값이 x*가 된다.
영상에서 contraction mapping function은 √x(루트 x) 이고 이를 무한정 반복한 결과 x*는 1임을 직관적으로 이해할 수 있다.
이것을 Banach fixed point theorem 관점으로 다시 설명해보자면
- non-empty complete metric space인 실수집합 R과, R상에서 거리를 정의하는 유클리디안 distance d가 존재한다. (R,d)
- 그리고 Contraction Mapping Function T(x) = √x이다.
- 이때 xn+1 = T(xn)이라 정의하고 함수 T에 대해 sequential하게 xn (n = 1, 2, 3 ...)을 계속해서 대입하다보면 (계산기에서 엔터를 무한정 반복한 행위)
- T(x)에 대해 T(x) = x인 유일한 solution을 찾게 된다. (현재 함수 T에 대해서는 그 solution==1인 것이다.)
'Background > Math' 카테고리의 다른 글
- Total
- Today
- Yesterday
- 3b1b
- antigen antibody interaction prediction
- 선형대수
- 3B1B따라잡기
- elementry matrix
- 기계학습
- ai신약개발
- 백준
- 최대우도추정
- 인공지능
- 이왜안
- eigenvalue
- Matrix algebra
- Manimlibrary
- 파이썬
- nanobody
- marginal likelihood
- MatrixAlgebra
- 논문리뷰
- manimtutorial
- MorganCircularfingerprint
- 항원항체결합예측모델
- 베이즈정리
- 오일석기계학습
- eigenvector
- manim
- manim library
- MLE
- 나노바디
- dataloader
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
