티스토리 뷰
https://www.youtube.com/watch?v=VH0TZlkZPRo
Jacobi iteration method
보통 linear algebra에서 Ax = b 형태의 문제를 푸는데 A, x, b 의 사이즈가 커지면 커질수록 time complexity와 memory complexity가 기하급수적으로 커지게 된다. 따라서 이러한 경우 문제를 jacobi iteration 방법을 통해서 x를 approximation하여 훨씬 효율적으로 문제를 풀 수 있도록 한다.
Diagonally Dominant Matrix
Jacobi method는 Matrix A가 Diagonally dominant 할 때만 사용하는 것이 좋다고 한다. 그렇지 않을때는 오히려 iteration에 의해서 찾고자 하는 solution vector x가 converge 하지 않고 발산하는 경우가 많은가 보다.
Diagonally dominant matrix는 간단하다. 다음의 성질을 만족하는 matrix이다.

3 x 3 matrix 하나만 그려서 잠깐 생각해 보면 충분히 이해할 수 있을테니 따로 예시를 들진 않겠다.
Iteration method
(1) 반복법 자체는 그리 어렵지 않다. 다음과 같은 Ax=b equation system이 존재한다고 하자.
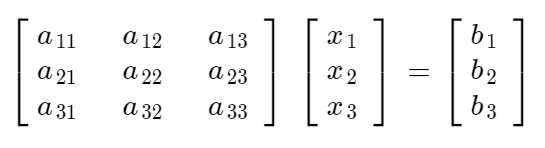
(2) 이것을 풀어쓰면 다음과 같이 나타낼 수 있다.
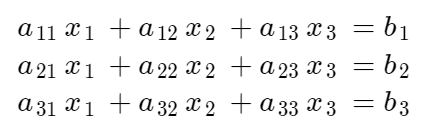
(3) 이제 각 줄로부터 x1, x2, x3만을 좌항에 남겨두고 모두 우항으로 정리하면 다음과 같은 식을 얻을 수 있다.

(4) 이제 x1 ~ x3을 random intialization 한뒤 다음과 같은 iteration을 진행한다.

(5) 각 스텝별로 x에 대한 오차를 확인한다.

이제 equation (4)를 반복하면서 equation (5)의 오차가 설정한 threshold 이하로 떨어져 충분히 converge 되었다고 판단될 때까지 반복해주고 x를 결정해주면 된다.
상당히 이해하기에 명료한 approximation method라 쉽게 공부할 수 있었지만 Deep Learning 관점에서 어떻게 적용해야 하는가를 모르겠다. Deep learning 관점에서 우리는 x를 업데이트 하는 method가 필요한게 아니라 Matrix A를 optimization 하는게 아닌가? GNN original paper에서 jacobi method가 언급되어 공부를 하긴 했으나 어떻게 적용해야 할지는 잘 이해가 되지 않는다. 이것은 추후에 조금 더 찾아보고 이해가 된다면 수정하여 작성해보자.
'Background > Math' 카테고리의 다른 글
- Total
- Today
- Yesterday
- eigenvector
- marginal likelihood
- dataloader
- 3b1b
- antigen antibody interaction prediction
- 이왜안
- MatrixAlgebra
- elementry matrix
- Manimlibrary
- 3B1B따라잡기
- 기계학습
- 백준
- nanobody
- Matrix algebra
- 인공지능
- ai신약개발
- MLE
- 베이즈정리
- manimtutorial
- 나노바디
- 항원항체결합예측모델
- eigenvalue
- 선형대수
- manim
- 최대우도추정
- 오일석기계학습
- 논문리뷰
- MorganCircularfingerprint
- 파이썬
- manim library
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
