티스토리 뷰
1-1. 베이즈 추정을 이용하면 '쇼핑족'과 '아이쇼핑'족을 판별할 수 있다.
비즈니스에서 실제로 사용될법한 예를 들어 설명해보자, 상품 판매원이 어떤 손님이 들어왔을 때 가장 신경써야 할 부분은 이 손님이 '실제로 지금 매장에서 구매 의사가 있는 손님인가'여부이다.
이렇게 '손님이 실제로 구매 의사가 있는가'를 판단하는 기준은 상당히 모호하지만, 만약 이것을 수치화 할 수 있다면 판매원은 그 기준을 통해 추후 행동을 결정하는데 큰 도움을 받을 수 있을 것이다.
1-2. [1단계] 경험으로부터 '사전확률'을 설정한다.
눈 앞에 손님이 있는 상황을 가정한다. 이 때 베이즈 추정을 이용해 해당 손님이 쇼핑족인지, 아이쇼핑족인지 판단하기 위해 가장먼저 해야하는 일은 '경험으로부터 얻어진, 손님들 중 쇼핑족과 아이쇼핑족의 비율이 얼마나 되었는지를 결정하는 것' 이다. 그리고 이 확률을 우리는 베이즈 통계학에서 사전확률(prior probability)이라고 부른다.
사전확률이란 어떤 '정보'가 들어오기 전, 경험에 의해 설정한(또는 무작위로 설정한) 확률이다.
그리고 여기서 말하는 정보는 예를들어 지금과 같은 상황에서는, 손님이 '말을 거는 행동을 하다', '특정 상품의 가격을 물어보다' 와 같은 추가적인 상황에 대한 정보를 얻는 것을 이야기한다.
만약 손님이 판매원에게 '말을 거는 행동'을 추가적으로 했다면, 우리는 이 추가적인 정보를 이용해 이 손님이 쇼핑족인지, 아이 쇼핑족인지를 판단하던 기준을 업데이트할 수 있게 된다.
예를 들어 여기서 경험에 의해 손님 열 명중 두명은 실제로 물건을 구매하였고, 나머지 여덟은 물건을 구매하지 않았다고 판단한다면, 이때의 사전확률은 P(쇼핑족) = 0.2, P(아이쇼핑족) = 0.8이 된다.
이 사전 분포를 면적에 대한 그림으로 나타내면 도표 1-1과 같다.
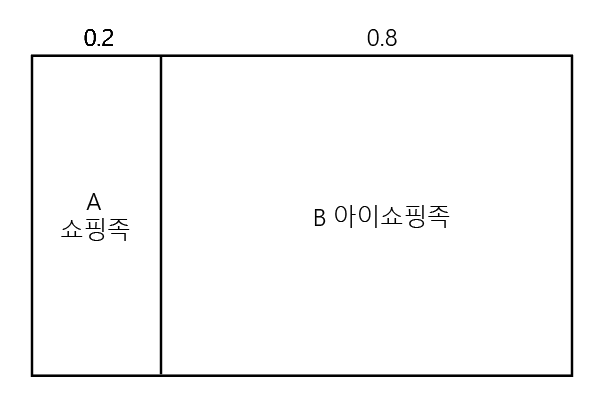
면적은 베이즈 확률을 다루는데 중요한 역할을 하게되니 앞으로 공부하는 내용은 노트에 직접 그려가면서 면적을 통해 베이즈 확률에 대한 이해를 돕도록 하자.
이 그림을 '둘로 분기된 세계'라고 생각하자, 내가 마주한 손님은 A나 B 둘중 하나인 것은 100% 확실하지만, 어느쪽에 속하는지는 모르는 상태인 것이다.
추가로, 왜 굳이 0.2와 0.8인가? 이것은 확률의 개념에 의한 것이고, 확률은 기본적으로 나타날 수 있는 모든 확률을 더했을 때, 그 값은 1이 된다는 수학적인 공리에 의한 것이다. 이 조건을 우리는 '정규화 조건'이라고 부를 것이다.
1-3. [2단계] 타입별로 '말거는' 행동을 하는 '조건부 확률'을 설정한다.
다음으로, 쇼핑족과 아이쇼핑족에 속하는 각각의 손님들이 어느 정도의 확률(분포)로 점원에게 '말걸기'라는 행동을 하는가를 설정한다.
이 조건부 확률은 사전확률이 경험에 의거한 데이터가 없어도 할당 할 수 있었던 것과 다르게 경험, 실증, 실험을 기반으로하는 실질적인 수치가 반드시 필요하다.
이것의 예시를 다음 표 처럼 나타내자.
| 타입 | 말을 걸 확률 | 말을 걸지 않을 확률 | |
| 쇼핑족(A) | 0.9 | 0.1 | → 1 |
| 아이쇼핑족(B) | 0.3 | 0.7 | → 1 |
| ↓ 1.2 |
↓ 0.8 |
표를 가로로 보면, 위에서 언급했던 '정규화 조건'을 충족하는 것을 볼 수 있다, 반면 세로 방향으로는 정규화 조건을 충족하지 않는다. 헷갈릴 수 있겠지만, 이것은 자명한데 표의 가로방향은 '특정한 하나의 세계에 속하는 손님이 특정한 행동을 할 확률' 이므로 특정 행동을 할 확률을 모두 더하면 이것은 반드시 1이 되어야 한다.
반면 표를 세로방향으로 본다면, 우리는 손님을 나누는 세계의 기준을 '말을 걸 손님'과 '그렇지 않은 손님'으로 나눈 것이 아니기 때문에 말을 걸고 그렇지 않고를 기준으로 바라보는 사건은 전체 행동을 아우르는 확률이 아니다. 때문에 더했을 때 반드시 1이 될 이유가 없다.
여기서 나오는 확률들은 모두 '조건부 확률'이다. 조건부 확률이란 '원인을 알고있을 때, 결과의 확률'인데 여기서는 '손님의 타입을 한정했을 경우, 각 행동을 할 확률'이 된다. 손님의 타입을 '원인'으로 생각한다면, 행동의 확률이 '결과'가 되는 것이다.
이것을 도표로 나타내면 [도표 1-2]와 같다.
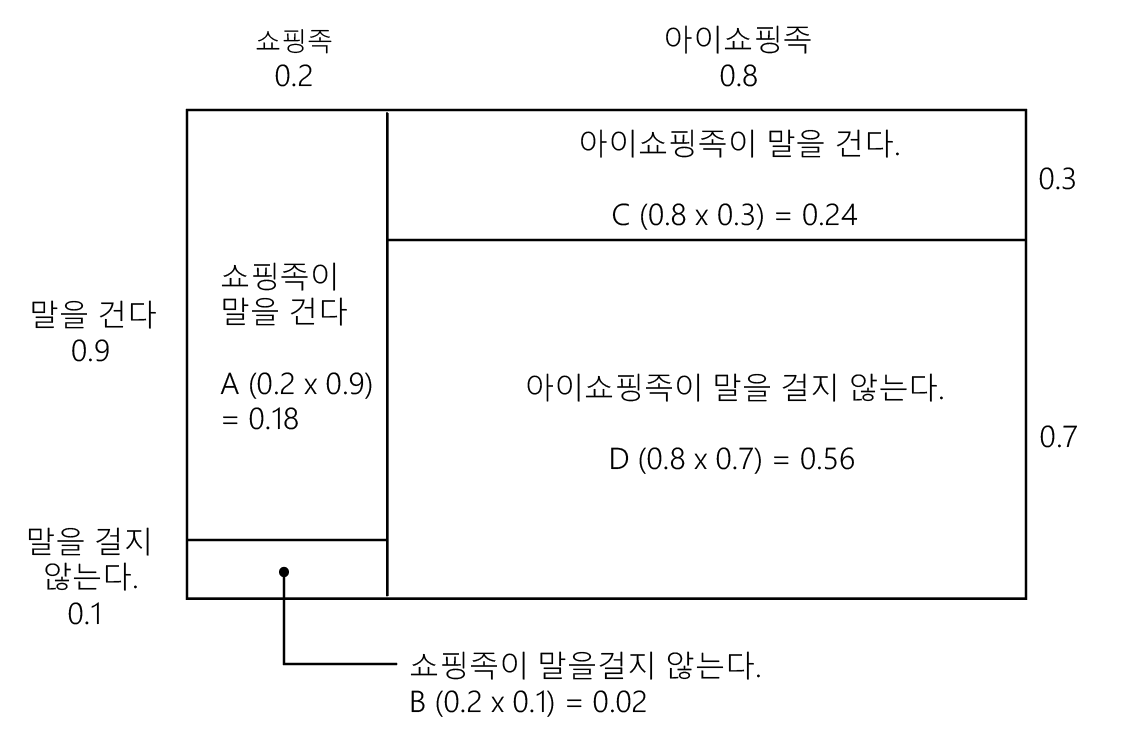
각각의 확률을 모두 더하면 0.18 + 0.02 + 0.24 + 0.56 = 1이 되는 것을 확인 할 수 있다.
1-4. [3단계] 관측한 행동으로부터 '가능성이 사라진 세계'를 제거한다.
한단계 더 나아가보자, 손님이 판매원에게 '말을 거는' 행동을 했다고 하자. 당신은 손님의 한가지 행동을 관측한 것이다. 이것이 상황에 대한 추가적인 정보가 된다고 1-2에서 이야기했다.
여기서 추가적인 정보는 손님이 '말을 걸지 않는다'는 세계는 발생할 확률이 없어졌다는 것을 의미하고, 4개로 분기되어있던 세계로부터 '말을 걸지 않는다' 는 세계들은 사라져도 무관하다는 것을 의미하게 된다.
이것을 다시 도표로 나타내면 [도표 1-3]과 같다.
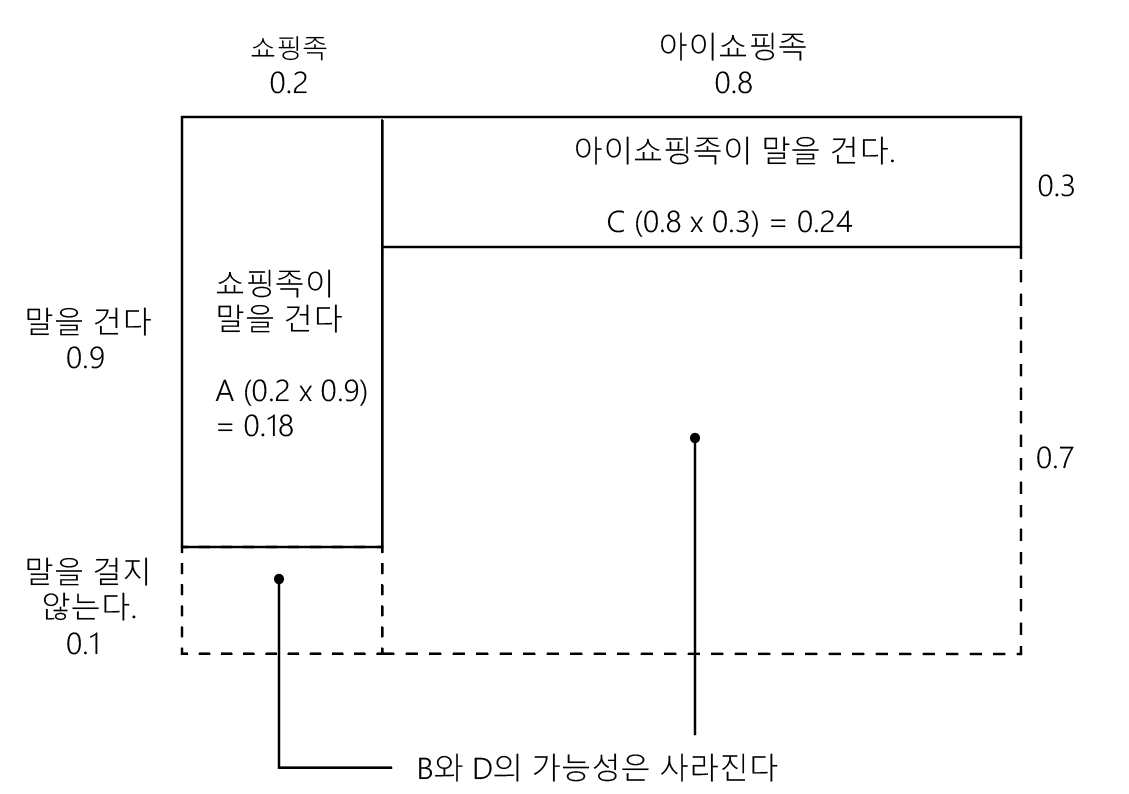
말을 걸지 않는다는 행동을 하던 세계는 사라졌다.
1-5. [4단계] '쇼핑족'의 '베이즈 역확률(사후확률)'을 구한다.
앞에서 손님이 '말을 건다' 는 행동을 관측함으로부터 가능세계는 두가지로 한정되었다. 즉, 손님은 쇼핑족이면서 말을 걸다, 또는 아이쇼핑족이면서 말을 걸다라는 두가지 세계중 반드시 하나로 속하게 된다. 그런데 도표 1-3을 들여다보자, 우리는 앞에서 확률의 합계는 반드시 1이 되어야 한다는 '정규화 조건'을 이야기했다. 여기서 세계의 합이 1이 되지 않기 때문에 A 사건과 C 사건의 비율을 그대로 유지하면서 두 사건의 합이 1이 되도록 확률을 다시 계산해보면
A : C = 0.18 : 0.24 = 3 : 4이고 두 사건의 합이 1이 되어야 하므로 양 변을 7로 나눠주면
A : C = 0.42 : 0.58이 된다.
즉, 기존에 아무런 정보가 없을 때, 우리는 이 손님이 쇼핑족일 확률을 0.2로 설정했었다.(사전확률) 그러나 손님이 말을 걸어온다는 행동에 대한 관찰로부터 정보를 얻고, 우리는 해당 손님이 쇼핑족일 확률을 0.42로 2배 가량 업데이트 할 수 있게 된 것이다. (베이즈 갱신)
이때 업데이트 된 확률을 우리는 '베이즈 역확률'또는 '사후확률'이라고 부른다.
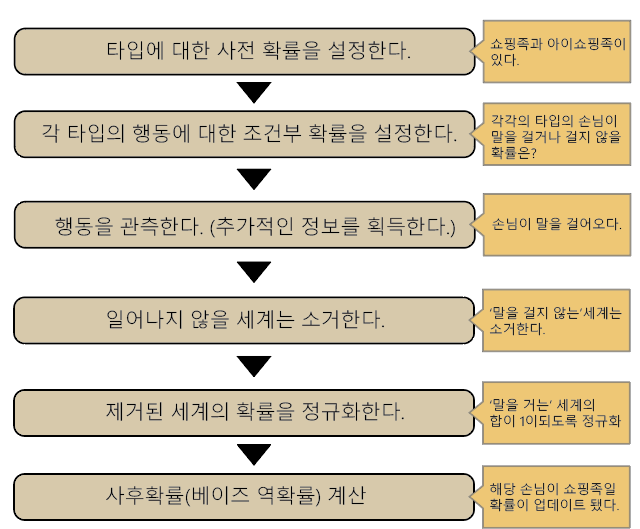
1-6. 베이즈 추정의 프로세스 정리
'Background > Statistics' 카테고리의 다른 글
| Bayesian Decision Theory 공부 정리(1) - 이해에 필요한 배경지식 (1) | 2023.04.21 |
|---|---|
| 1부) 베이즈 통계학 기초 -4.'확률의 확률'을 사용하여 추정의 폭을 넓힌다. (0) | 2023.03.30 |
| 1부) 베이즈 통계학 기초 -3.주관적인 숫자여도 추정이 가능하다. [발렌타인데이 초콜렛 문제] (0) | 2023.03.30 |
| 1부) 베이즈 통계학 기초 -2.베이즈 추정은 때로는 직감과 완전히 다른 결과를 보인다. (0) | 2023.03.29 |
| [베이즈통계학] 1) 베이즈 통계학의 개념을 이해하자 (0) | 2023.03.27 |
- Total
- Today
- Yesterday
- ai신약개발
- 기계학습
- Manimlibrary
- eigenvalue
- 오일석기계학습
- MorganCircularfingerprint
- kld
- 3b1b
- nanobody
- marginal likelihood
- 최대우도추정
- 파이썬
- 나노바디
- 백준
- 베이즈정리
- 선형대수
- kl divergence
- manim library
- eigenvector
- 제한볼츠만머신
- manim
- MatrixAlgebra
- 이왜안
- MLE
- 인공지능
- manimtutorial
- Matrix algebra
- 3B1B따라잡기
- variational autoencoder
- elementry matrix
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
