티스토리 뷰
선형대수학 Orthogonality and Least Squares 정리/모음 (1) - Inner Product, Length, and Orthogonality
벼랑끝과학자 2023. 6. 11. 01:21Vector는 소문자 bold체로 나타냅니다(v) 소문자이면서 bold체가 아닌 경우(a)는 상수를 나타냅니다.
제곱이나 아래첨자를 업데이트 하지만 티스토리 블로그 특성상 작성이 불편하기 때문에 오타가 있을 수 있습니다.
구체적인 내용에 대한 전달이 아니라 기초적인 선형대수학의 정리를 모아놓는 포스팅입니다.
작성되는 포스팅은 모두 인프런 - 타블렛깍는노인 조범희님의 강의를 바탕으로 작성했습니다.
이전 시리즈
2023.05.25 - [Background/Math] - 선형대수학 Linear Algebra 용어 및 기초 이론 정리/모음
지금까지 Ax = b를 푸는 방식을 배웠는데 실제 실험 데이터서는 Ax = b를 정확히 만족하는 해는 보통 없다. 따라서 x대신 이를 근사하는 x^(x hat)를 찾는다. 다시말해 b에 최대한 가까워지는 x^를 찾는것이다.
이때 Least Square는 Ax^와 실제 정답 b의 차이를 최소화 하는 방법이다.
- Inner Product(내적) : 다음과 같은 벡터 u와 v가 있다고 하자.
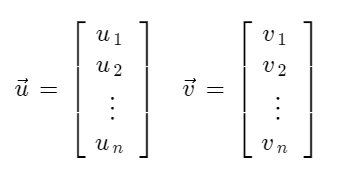
이때 u와 v의 innerproduct = uTv 이다. u와 v의 순서는 바뀌어도 상관없다. 이때 uTv 를 u ∙ v로 표현한다.
정리1.
u, v, w ∈ Rn 이고 c는 scalar일때, 다음을 만족한다.
- u ∙ v = v ∙ u
- (u ∙ v) ∙ w = u ∙ w + v∙ w
- (cu) ∙ v = c(u ∙ v)
- u ∙ u 는 반드시 0보다 같거나 크고, 만약 u ∙ u가 0이면 u는 반드시 0벡터이다.
- Length of a Vector : vector의 length는 다른말로 norm이라고 표현한다. 반드시 0이상의 scalar value이며 다음과 같이 나타낸다. 앞으로는 norm으로 통일하자.
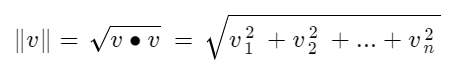
R2 space에서의 norm은 우리가 흔히 알고 있는 유클리디안 거리와 같은 개념이다. 그리고 ||cv|| = |c|||v||이다. 즉, norm에 음수를 곱하여도 거리는 양수배가 된다.
- unit vector : 임의의 vector의 norm을 1로 scaling한 벡터 또는 임의 벡터의 norm = 1인 벡터 즉 ||u|| = 1인 벡터 u
- normalization : 임의의 vector u의 norm을 1로 scaling하는 행위를 normalization이라 하며 다음과 같다.

u와 v는 같은 방향을 가지는 벡터가 되고 u는 norm = 1인 벡터가 된다.
- Distance : Rn space의 vector u와 v를 생각해보자, 두 벡터 사이의 거리를 dist(u, v)로 표현하며 dist(u, v) = u - v의 norm이다. (또는 v - u 의 norm)
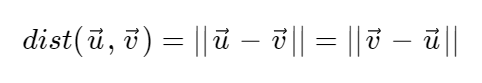
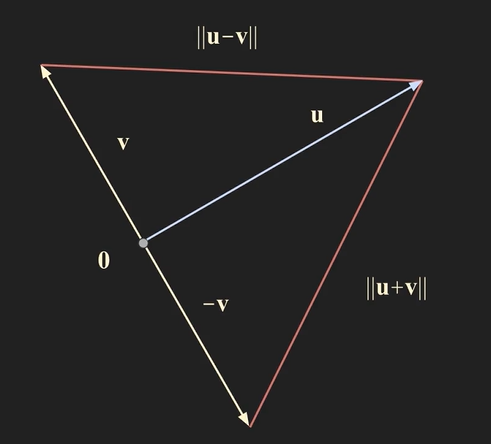
- Orthogonal vector : 두 벡터 사이의 inner product가 0일 때, 두 벡터를 orthogonal하다고 한다. 따라서 Zero vector는 그 어떤 벡터와도 orthogonal하다.
정리2.
두 벡터 u와 v가 orthogonal하다. if and only if ||u + v||2 = ||u||2 + ||v||2
- orthogonal complements : 다음과 같은 이미지를 생각해보자.
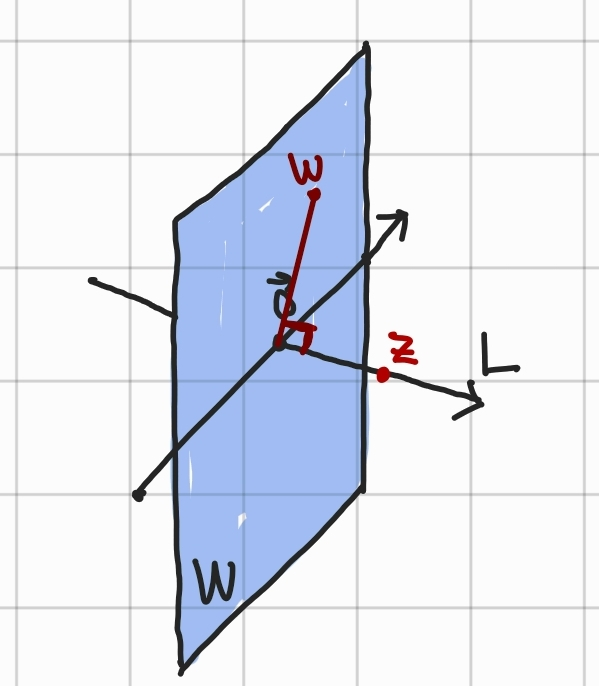
- W를 R3 space에 존재하는 subspace이며 원점을 지나는 평면(plane)이라 하자.
- L을 원점을 지나면서 W에 수직인 직선이라 하자.
- 이때 L과 W가 서로 수직이기 때문에 L위의 임의 벡터 z와 W위의 임의 벡터 w의 inner product는 반드시 0이다. 즉, orthogonal하다.
- 또한 임의 벡터 z가 모든 W위의 벡터 w와 orthogonal하다면 z는 subspace W에 orthogonal하다고 할 수 있다.
- 이런 subspace W에 orthogonal한 모든 임의 벡터 z의 set을 orthogonal complements of W라고 하고 W⊥로 표기한다.
정리3.
(Row space A)⊥ = Null A이고 (Col space A)⊥ = Null AT이다.
'Background > Math' 카테고리의 다른 글
- Total
- Today
- Yesterday
- 이왜안
- MLE
- elementry matrix
- 오일석기계학습
- marginal likelihood
- ai신약개발
- 최대우도추정
- antigen antibody interaction prediction
- manim library
- Matrix algebra
- 항원항체결합예측모델
- eigenvalue
- dataloader
- 나노바디
- manimtutorial
- 3B1B따라잡기
- 3b1b
- MorganCircularfingerprint
- nanobody
- eigenvector
- 베이즈정리
- 논문리뷰
- 선형대수
- 백준
- MatrixAlgebra
- Manimlibrary
- 기계학습
- 인공지능
- 파이썬
- manim
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
