베르누이 시행과 확률변수

본 내용은 모두 KMOOC 여인권 교수님의 통계학의 이해 I 수업의 내용을 기반으로 작성됩니다.

http://www.kmooc.kr/courses/course-v1:SookmyungK+SM_sta_004k+2019_03SM_02/course/ 

강좌 | SM_sta_004k | K-MOOC

 

1. 베르누이 시행 (Bernoulli trial)

a) 각 실험에서 발생 가능한 결과는 2가지
    ex) (성공S, 실패F) / (앞면, 뒷면) / (불량, 정상)...
b) 각 실험은 독립적으로 수행된다.
c) 모든 실험 결과의 확률은 항상 동일하다
    ex) P(성공) = p 일때 P(실패) = 1-p = q 

 

예를들어 불량품 검사를 시행해보자

10개의 제품 중 3개가 불량품이고 2개를 복원추출하는 경우는 베르누이 시행인가?

a) 발생가능한 결과는 2가지인가? --> (불량, 정상) --> Yes

b) 각 실험은 독립적으로 수행되는가? 

c) 모든 실험 결과의 확률이 항상 동일한가?

두 사건 A와 B가 독립인지 확인하기 위한 식

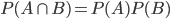
여기서 불량품을 뽑는 사건을 P(S)라고 하자, 이때 P(S) = 3/10이다.

복원 추출의 경우 P(S1∩S2)는 P(S1)P(S2|S1)이고 3/10 x 3/10이므로 복원 추출의 경우일 때

a) 불량품을 뽑는 시행은 P(S1)P(S2) = 3/10 x 3/10과 같아 독립이다.
b) 그리고 모든 실험 결과의 확률이 항상 동일하므로 베르누이 시행이다.

 

그러나 복원추출이 아닐 경우 P(S2) = 3/10인데 P(S2|S1) = 2/9이므로 두 사건은 독립이 아니다.

 

모집단의 크기가 충분히 크고, 표본의 수가 작을 경우 베르누이 시행으로 인정하기도 한다.

 

그러나 비복원 추출의 경우더라도, 모집단의 크기가 상당히 크고, 내가 뽑은 표본의 크기가 작은 경우에는 엄밀하게 따져서는 베르누이 시행이라고 할 수 없지만, 편의를 위해 베르누이 시행의 근사 모형으로 인정하기도 한다.

2. 베르누이 확률 변수의 Probability Mass Function(PMF)는 아래식과 같다.

확률변수가 베르누이 분포를 따를 때

​

 

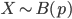
3. 베르누이 확률 변수의 성질

a) E(X) = p
b) Var(X) = p - p²
c) SD(X) = √Var(X)