티스토리 뷰
본 내용은 모두 KMOOC 여인권 교수님의 통계학의 이해 I 수업의 내용을 기반으로 작성됩니다.
개인 공부를 위해 수업의 내용을 정리할 뿐이고, 완벽한 이해를 바탕으로 작성되지 않는 부분도 있습니다.
http://www.kmooc.kr/courses/course-v1:SookmyungK+SM_sta_004k+2019_03SM_02/course/
강좌 | SM_sta_004k | K-MOOC
www.kmooc.kr
1. 이항분포 (Binomial distribution)
: 성공할 확률이 p인 베르누이 실험을 n번 반복했을 때, 성공 횟수(X)의 분포

예를들어 동전던지기를 8번 시행해서 다섯번 앞면이 나왔다고 하자, 이때 성공횟수 5번을 8번의 베르누이 확률변수의 합으로 나타낼 수 있다. (X1 + X2 + ... + Xn) = 5
2. 이항분포의 기댓값
이항분포의 경우 베르누이 확률분포에서 계산했던 기댓값을 이용하면 쉽게 이항분포의 기댓값을 계산할 수 있다.
a) X ~ B(p)의 경우 E(X) = p, Var(X) = p(1-p)였다.
b) 이항확률변수 X의 기댓값 E(X) = E(X1 + X2 + ... + Xn) = E(X1) + E(X2) + ... + E(Xn) = n * p
c) 베르누이 시행은 독립시행이므로 두 사건의 Cov(A,B) = 0이다.
Var(X + Y) = Var(X) + Var(Y) + 2*Cov(A,B) 또는
Var(X - Y) = Var(X) + Var(Y) - 2*Cov(A,B) 이다.
그런데 독립 사건의 경우 Cov(A,B) = 0이므로
베르누이 시행 또는 이항확률분포에서 Var(X) = Var(X1 + X2 + ... + Xn) = Var(X1) + ... + Var(Xn) = np(1-p)
d) SD(X) = √Var(X)
3. 이항분포의 확률질량함수(probability mass function)
베르누이 시행의 확률 질량함수는 아래식과 같았다.

이항분포의 확률 질량함수는 어떻게 표현할 수 있을까?
주사위를 세번 던졌다, X = 1이 나온 횟수라고 하자 1이 나오면 S 1이외의 숫자가 나오면 F로 표시하자 이때 시행을 통해 얻어지는 표본 공간은 아래와 같다.

이걸 일반화 시켜서 이야기하면 시행횟수가 n, 성공확률이 p인 이항분포의 확률 질량함수는 아래와 같다.

이항분포의 모양은 n과 p가 결정하며 이때 두 값을 모수(parameter)라고 한다. 따라서 베르누이 시행은 X ~ B(p)라고 표시했던것과는 다르게 이항분포의 경우에는 아래와 같이 표현한다.

단 여기서 B는 Bernoulli의 의미가 아니라 Binomial의 B이다.
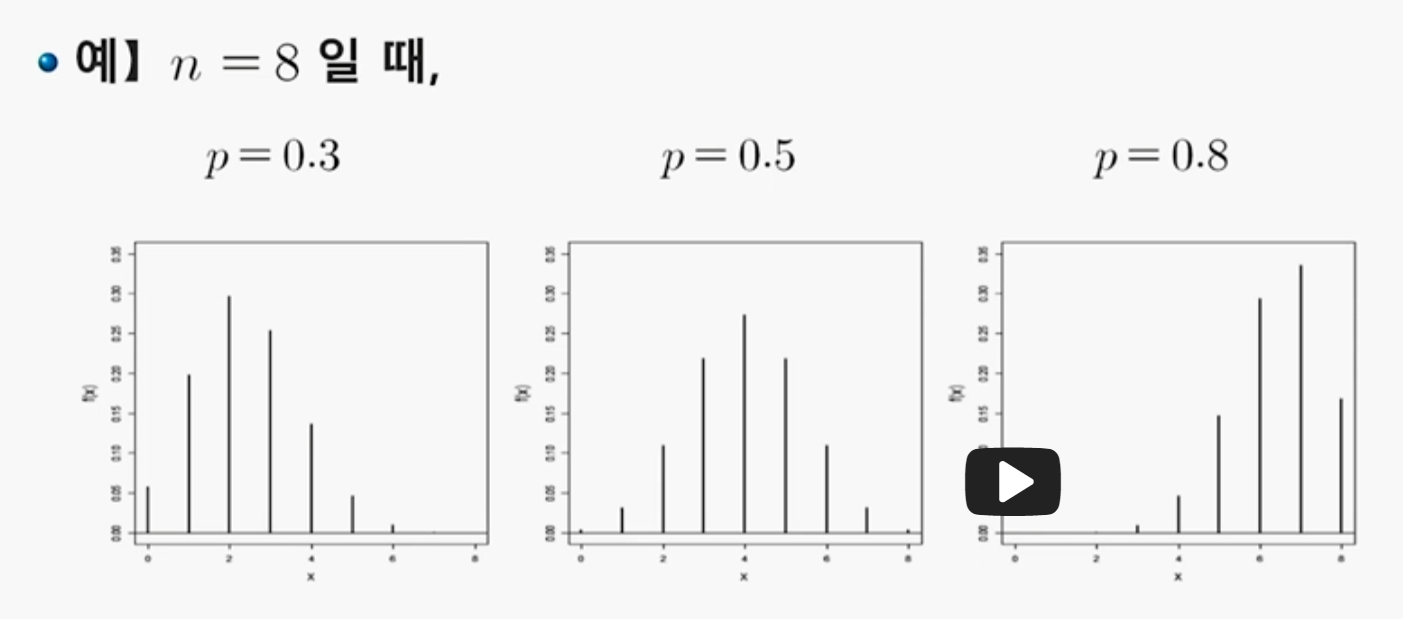
통계학에서는 주로 모집단의 p값을 모르고 표본의 분포만 확인할 수 있기 때문에 표본의 분포로부터 모수 p를 추정하는 문제를 주로 다룬다고 한다.
4. 이항분포의 특성
a) X ~ B(p) , Y ~ B(p)이고 X, Y가 독립이면 X + Y ~ B(2, p) 단, 여기서 B는 베르누이
b) X ~ B(m,p), Y ~ B(n,p)이고 X ,Y가 독립이면 X + Y ~ B(m+n, p)
근데 시행횟수가 1000~ 등 무수히 많아지기 시작하면? 어떻게 계산을 하는가? --> 어떠한 다른 근사값을 이용해 다시 계산을 하는데 여기서는 일단 넘어간다.
'Background > Math' 카테고리의 다른 글
| 최대우도 추정1 (Maximum Likelihood Estimation) (0) | 2023.01.24 |
|---|---|
| 독립 (Independence) (0) | 2023.01.24 |
| 조건부 확률 (Conditional probability) (0) | 2023.01.20 |
| 정규분포 (Norminal distribution) (0) | 2023.01.16 |
| 베르누이 시행과 확률변수 (0) | 2023.01.11 |
- Total
- Today
- Yesterday
- manimtutorial
- 백준
- marginal likelihood
- 나노바디
- 기계학습
- manim library
- 선형대수
- 베이즈정리
- nanobody
- MLE
- dataloader
- 논문리뷰
- MatrixAlgebra
- eigenvalue
- 인공지능
- antigen antibody interaction prediction
- 3b1b
- 이왜안
- MorganCircularfingerprint
- 오일석기계학습
- manim
- 파이썬
- elementry matrix
- eigenvector
- ai신약개발
- Matrix algebra
- 항원항체결합예측모델
- Manimlibrary
- 3B1B따라잡기
- 최대우도추정
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
