[2022 NIPS] DIffAb 공부 (1)

https://www.biorxiv.org/content/10.1101/2022.07.10.499510v5

Antigen-Specific Antibody Design and Optimization with Diffusion-Based Generative Models for Protein Structures

 

DIffAb는 Diffusion based model을 이용해서 Antibody(이하 Ab) generation을 목표로 한 최초의 연구다. 

DiffAb는 NIPS에 2022년도에 발표되었다. 그 직전에 2022 ICLR에 Ab서열과 구조를 co-design하는 것을 목표로 하는 GNN기반의 연구(RefineGNN, https://doi.org/10.48550/arXiv.2110.04624)가 발표되기는 하였으나 해당 연구는 molecule또는 protein등의 3D 구조체를 다루는 연구에서 반드시 지켜져야 하는 중요한 특성인 invariant와 equivariant 성질을 입증하지 못했다는 치명적인 단점이 있다.

DiffAb는 이런 직전의 연구의 단점을 보완하여 더 명확한 Ab generation 학습 전략을 이용한 모델을 제안한다.

 

Introduction

대부분 Ab generation을 목표로 연구된 논문들의 introduction은 다음 내용들이 주를 이룬다.

• Ab의 구조에 대한 간단한 설명 (FR과 CDR등에 대한)
• 기존 wet-lab 기반 연구의 한계점 지적 
• 컴퓨터를 이용한 기존 Molecular dynamics based 연구들의 한계점 지적
• DL-based 연구의 필요성 강조

DiffAb도 별반 다르지 않아 이부분은 넘긴다. 

DiffAb는 직전의 Ab seq-structure co-design 문제를 다룬 RefineGNN이 두가지 문제를 잘 다루었다고 이야기한다.

• CDR 서열을 어떻게 3D 구조화 할 것인가?
• CDR 제외한 나머지 부분을 condition으로 하여 어떻게 CDR의 distribution을 modeling할것인가?

그러나 이것만으로는 부족함을 지적하며 Ab generation에서는 다음과 같은 세 가지 고려사항을 반드시 추가해야함을 강조한다.

• CDR 디자인은 '명확하게' target Antigen (이하 Ag)과의 3D interaction을 조건으로 받고 구성되어야한다.
• 보통 단백질간의 결합은 아미노산 그 자체가 아니라 아미노산(AA)에서 side chain으로 나와있는 R기에 의해 결정되므로 AA의 position뿐 아니라 R기의 orientation도 반드시 고려되어야 한다.
• 보통 Ab는 아주 새로운 de novo 디자인을 하는게 아니라, 하나의 인간화 되어있는 기본 구조로부터 원하는 target에 BA가 높은 CDR서열을 갖는 Ab로 최적화하여 찾아가는 과정을 통해 생성한다. 따라서 from scratch de novo design보다 현실적인 방법인 CDR optimization을 따르는 것이 좋다.

위에서 말한 세 가지 고려사항을 고려하면서 sequence와 structure를 함께 jointly sampling할 수 있는 diffusion-based Ab generation model을 연구하는 것이 본 논문의 핵심 problem이 된다.

최종적으로 저자들은 본 연구의 contribution을 다음 세 가지로 요약한다.

1. Ag의 3D구조를 명확하게 조건부로 입력한 최초의 CDRs 생성모델
2. AA의 Side-chain의 orientation까지 고려한 Atom level Ab design한 최초의 모델
3. 서열-구조 co-design뿐 아니라 현실의 task와 일맥상통하는 fix-backbone CDRs dsign과 Ab optimization 제안

 

Related Work

이부분은 자세히 설명하지 말고 언급한 연구에 대해서만 간단히 언급하고 넘긴다.

Computational Ab Design
2022 ICLR의 RefineGNN, 그 외는 너무 옛날 Molecular Dynamics 기반의 모델이라 생략

Protein Structure Prediction
Roesttafold, AlphaFold, trRosetta 등 언급

DDPM
최근에는 equivariant까지 고려한 molecular 3D 생성모델 [Learning gradient fields for molecular conformation generation, Equivariant diffusion for molecule generation in 3d, Torsional diffusion for molecular conformer generation, Geodiff: A geometric diffusion model for molecular conformation generation] 등 다수 개발중

유클리디안 공간이 아닌 리만공간에서의 모델들도 있음 [Denoising diffusion probabilistic models on so (3) for rotational alignment, Riemannian score-based generative modeling]

discrete categorical data에 대해서도 DDPM은 적용 가능함 [Argmax flows and multinomial diffusion: Learning categorical distributions, Structured denoising diffusion models in discrete state-spaces]

위와 같은 모델들의 개발에 이어서 단백질에 적용된 DDPM모델도 개발되었음 [Protein structure and sequence generation with equivariant denoising diffusion probabilistic models, Diffusion probabilistic modeling of protein backbones in 3d for the motifscaffoldi g problem, Protein structure generation via folding diffusion]

 

Method

기본적인 diffusion model에 대한 사전지식은 가지고 있다고 생각하고 작성합니다. DDPM에 대한 전반적인 이해가 되지 않으신 분들은 이해가 어려울 수 있습니다.

기본적으로 해당 연구는 단백질의 생성을 위해 3가지의 데이터에 대한 생성 후, AF 등의 3D 구조화 작업을 거쳐서 완성된 Ab를 생성합니다. 본 연구는 Framework Region(FR)은 생성하지 않으며 오직 Complemetary Determining Regions (CDRs)에 대한 데이터만을 생성합니다. 1...N까지의 전체 아미노산 서열 중, 중간 l 번째 아미노산부터를 CDRs로 생각하며, 거기로부터 m개의 CDRs 서열을 생성하는 task를 진행합니다. 따라서 1, 2, ... ,l과 l+m+1, ..., n까지는 FR 또는 Ag, Ab의 Constant region의 서열로 backborn으로 생각하며 논문에서는 C로 표기합니다. l+1, ... l+m까지를 우리가 생성해야하는 CDRs 부분으로 R로 표기합니다. 자세한 내용은 3.1 참고

생성되는 세 가지 데이터는 다음과 같습니다.

1. 아미노산 서열
2. 아미노산의 중심탄소의 x,y,z 좌표 (위치)
3. 아미노산의 R기의 방향 (Orientation)

이 세가지 데이터를 어떻게 diffusion 하고 de-noising하는지를 Method에서 설명합니다.

 

3-1. Definitions and Notations

이 부분은 notation을 정리한 부분이라 기호가 많이 필요해서 그냥 논문을 복사해다 붙여놓았습니다.

중요한건 우리가 생성해야 하는 CDRs은 R로, 그 외 조건부로 입력되어야하는 complex 데이터는 C로 표기한다는 것과 s, x, O가 각각 아미노산의 타입, alpha-Carbon (중심탄소)의 좌표, R기의 Orientation(방향) 임을 의미한다는 것을 기억하면됩니다.

 

3-2. Diffusion Processes

3-2-1. Multinomial Diffusion for Amino Acid Type

먼저 아미노산 서열에 대한 diffusion step은 다음과 같이 discriminated space에서의 Categorical distribution(논문에서는 Multinomial이라고 표현하였지만 Categorical로 표현하는게 익숙해서 Categorical로 표현합니다)을 이용해서 진행됩니다.

 

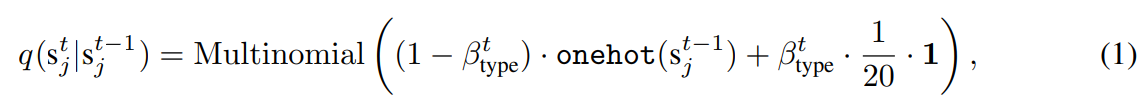
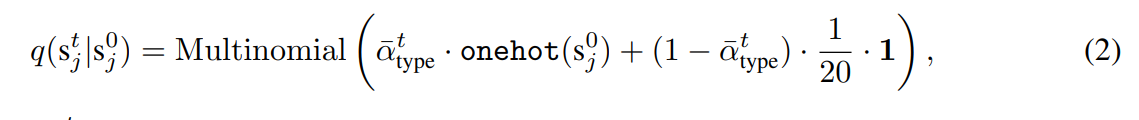
sj는 단백질이 1~n번째까지의 아미노산의 연결이라 했을때 j번째 아미노산 서열을 의미합니다. 위첨자 0, t, t-1등은 Diffusion의 t-step을 의미합니다. step이 의미하는 바가 무엇인지 이해되지 않는다면 Diffusion model의 개념부터 공부해야 합니다.

Eq(1)을 보면 t-1 step에서의 sj서열을 조건부로 t step에서의 아미노산 서열의 분포를 Categorical distribution으로 나타냈습니다. beta_type_t는 t가 0일때는 0에 가깝고 Large T로 갈 수록 1에 가까워집니다. 이를 직관적인 의미로만 생각하자면 t=0에 가까울때에는 기존 원본 단백질의 서열이 그대로 선택될 가능성이 매우 높은 distribution을, Large T로 갈 수록 20개의 아미노산 서열 종류가 선택될 확률이 모두 동일한 uniform distribution으로 이해하면 됩니다. 

Eq(2)는 DDPM에서 reparameterization trick을 이용해 t=0의 조건부로 t step에서의 분포를 나타내는 식을 그대로 보이고 있을 뿐입니다.

이제 DDPM논문을 잘 이해하고 있다면 베이즈 룰과 Eq(1)과 Eq(2)를 이용해서 우리가 원하는 Ground Truth분포를 approximately 계산할 수 있다는 것을 이해할 수 있을겁니다. 

Eq(3)는 Eq(1)과 Eq(2)를 이용해서 구한 Approximated Ground Truth 분포를 모델링(또는 surrogation)하는 분포라고 생각하면 됩니다. 모든 step에서의 Ground Truth distribution을 계산할 수 있으니 랜덤하게 추출된 step t에서 j번째 아미노산의 Categorical distribution을 예측하는 딥러닝 모델 F를 학습하면 됩니다. 딥러닝 모델 F는 j번째 아미노산 서열의 t-1 step의 denoising된 확률분포를 return합니다. t step의 CDRs서열의 정보와 전체 Complex 정보를 입력으로 받습니다.

Eq(4)를 통해서 아미노산 타입 예측값의 Loss를 계산합니다. 단순히 두개의 Categorical distribution의 KL divergence를 구하면 됩니다.

 

3-2-2. Diffusion for Cα Coordinates

Eq(6)은 오타가 있습니다. a_bar_pos는 0 step이 아니라 t step이어야합니다.

이부분은 말 그대로 DDPM 그대로 생각하면 됩니다. 이미지 데이터를 forward process를 이용해서 noisification한 뒤, denoisinig하는 학습 방법을 그대로 차용합니다. 정말 쉽게 직관적으로 이해하자면 해당 논문에서는 픽셀이 3개짜리인 이미지를 DDPM으로 학습하고 생성한다고 생각하면 됩니다.

DDPM의 모델 학습에 사용되는 Loss term으로는 대표적으로 t step만큼 noising된 이미지와 t step이라는 정보를 입력하여 원본 이미지 혹은 원본 이미지에 최초로 추가된 noise level 또는 score function을 예측하도록 하는 세 가지 방법이 있는데 해당 연구에서 사용된 Loss term은 이미지에 최초로 추가된 noise의 level을 loss로 채택하였습니다. (ϵ_j) 

이해를 쉽게하기 위해 이미지라고 말했지만, 실제로 딥러닝 모델 G는 아미노산 서열을 예측하는 딥러닝 모델이었던 F와 동일한 정보들을 입력으로 받고 j번째 아미노산의 Cα의 x,y,z 좌표를 return합니다.

아마도 DDPM에 충분히 익숙한 사람이라면 이 부분은 크게 문제없이 이해할 수 있을겁니다.

 

3-2-3. SO(3) Denoising for Amino Acid Orientation

이 부분이 해당 논문의 가장 핵심이 되는 Contribution이며, 상당히 이해하기에 까다로운 부분입니다. 
이 부분을 이해하기 위해서는 Appendix의 B part를 자세히 읽어봐야 합니다.

Appendix B.1 Preliminary: Axis-Angle Representation of Rotation

여기서 말하는 핵심은 본 연구는 물체의 회전을 표현하기 위해서 x,y,z 축에 대한 각도를 이용하는 오일러 각 표현법 대신 Axis-Angle 표현법을 사용한다는 것입니다. 왜 직관적이고 익숙한 3차원 좌표상의 오일러 각 표현법 대신에 직관적으로 바로 와닿지 않는 Axis-Angle 표현법을 사용해야 하는걸까?

오일러 각의 경우 짐벌락이라는 문제가 있다. 따라서 오일러 각을 사용하면 물체의 회전을 명확하게 나타낼 수 없습니다.
쉽게 말하면 x,y,z 축의 각각의 360°를 자유롭게 표현하지 못하는 문제가 있다. 이것을 말이나 그림으로 설명하기는 정말 어렵고 짐벌락이 무엇인지 이해하기 위해서는 블로그나 그림을 보기보단 아래 영상을 참고하는걸 300% 추천합니다.

https://www.youtube.com/watch?v=zc8b2Jo7mno

Axis-Angle 표현법은 또 무엇인가? 이것도 참 말로 설명하기 어려운데, 한번 어떤 물체를 손에 들고 회전을 시켜보자 이때 회전은 반드시 회전하는 축이 존재하고, 그 회전 축을 기준으로 반시계방향으로 몇도만큼 회전하는지는 반드시 결정되어있다. 이렇게 물체의 회전을 원점으로부터 결정되는 회전 축 벡터 e와 반시계방향으로의 회전량인 θ를 이용해서 나타낼 수 있다는 개념이 바로 Axis-Angle representation입니다.

아래 그림을 보면 지구본이 회전할 수 있는 축이 있고 해당 축을 기준으로 360도 자유롭게 회전할 수 있음을 이해할 수 있습니다. 지금 그림상의 지구본은 오직 하나의 정해진 축 방향 하나를 기준으로 회전하고 있지만 우리는 머리속에서 지구본의 축을 자유자재로 바꿔볼 수 있고, 그 변경된 축을 따라서도 마찬가지로 360도 자유로운 회전이 가능하다는 것을 알 수 있습니다. 이렇게 3차원 공간상의 모든 좌표의 어느 방향으로의 축 벡터를 형성할 수 있고, 모든 축을 기준으로 360도 회전을 해보면 지구본이 회전할 수 있는 모든 3차원 공간상의 회전을 표현할 수 있게됩니다. 

https://medium.com/data-science/3d-rotations-intuitions-and-limitations-f3ae2122fe23

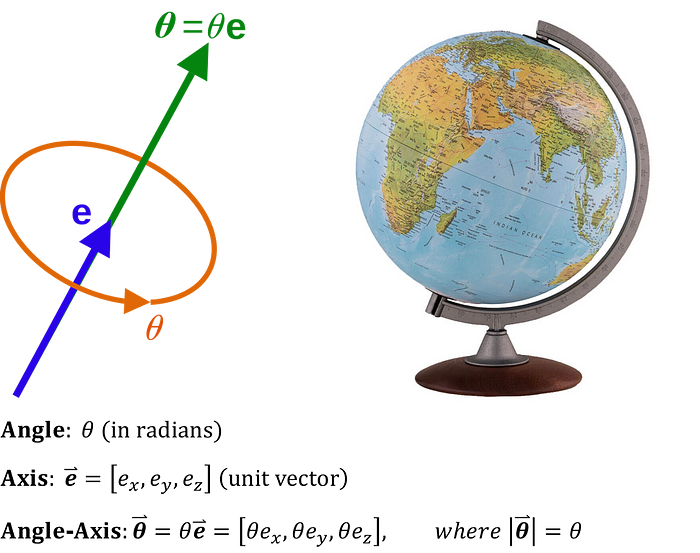
짐벌락 문제가 있는 오일러 각 표현법 대신 Axis-Angle representation 문제를 사용하면 또 장점이 있습니다. 회전을 표현하기 위해서 x,y,z 축 방향으로의 3가지 파라미터가 필요한 오일러 각보다 Axis-Angle 표현법을 사용하면 축 벡터 e와 회전량 θ만을 이용하므로 파라미터 2개로 회전을 표현할 수 있다는 점입니다. 저는 전공이 공학은 아니기에 깊은 수준의 Axis-Angle 표현법의 이해는 본 포스팅의 범위에서 벗어나므로 Axis-Angle 표현법이 더 궁금하신 분들은 아래 블로그들을 참고하시면 좋을 것 같습니다.

https://gaussian37.github.io/vision-concept-axis_angle_rotation/

축각 회전 (Axis-Angle Rotation) 또는 로드리게스 회전 (Rodrigues Rotation)

https://medium.com/data-science/3d-rotations-intuitions-and-limitations-f3ae2122fe23

3D Rotations: Intuitions And Limitations

 

B.2 Logarithm of Rotation Matrices and Exponential of Skew-Symmetric Matrices Logarithm of Rotation Matrices

Matrix의 logarithm이란 무엇인가요? 저는 공부하기 전까지만 해도 너무 당연히 그냥 행렬 내부의 요소들에 log를 취하는 거라고 생각했습니다만 전혀 아니었습니다.

Matrix logarithm은 일반적으로 n x n 정사각 행렬에 대해서만 정의되는 연산이며 일반적인 대각화 가능 행렬에 대해서는 대각화를 통한 로그화를(여기서는 다루지 않습니다), 특히 SO(3) group에 속하는 회전행렬(R)의 경우에는 다음과 같은 연산을 통해 계산이 가능합니다.

SO(3) group에 속하는 회전행렬이라는게 무엇을 말하는지에 대한 이해 역시 필요합니다. 그러나 본 포스팅에 SO(3) group에 대해 모두 설명하기에는 어려움이 있고 저 조차도 완벽하게 이해하지는 못하였습니다. 그러나 3차원 공간상에서 물체의 회전과 이동에 대한 중요한 개념인 SO(3)와 SE(3)에 대한 이해는 앞으로 단백질 생성 연구를 하려는 연구자에게는 필수적으로 짚고 넘어가야 할 개념이므로 다음 영상들을 통해 공부하시길 강력하게 추천합니다. 한국어로 설명된 영상중에는 가장 잘 설명해주신 영상이 아닌가 싶습니다.

https://www.youtube.com/watch?v=KzXjjNyktXk&list=PLddVNIYmpwlMIhcmqUAYL9-qvjPucZVrt

 

equation(21)

T는 행렬의 Transpose입니다. θ역시 구하는 방법이 나와있습니다. Tr은 Trace의 줄임말로 Tr(R) 이라 함은 행렬 R의 대각선 성분들의 단순 덧셈된 값을 의미합니다. 

결과적으로 로그화 된 행렬 R을 우리는 행렬 S라고 표현합시다. SO(3) group 행렬 R을 로그화한 행렬인 S는 so(3) group에 속한다고 말하며 반드시 skew-symmetric matrix형태를 하고있습니다. skew-symmetric matrix는 다음과 같은 형태의 행렬을 의미합니다. so(3) group에 대한 이야기 역시 본 

skew-symmetric matrix

 

여기서 행렬 S의 성분인 v_x, v_y, v_z를 이용해 구성된 벡터인 v = [v_x, v_y, v_z]가 우리가 위해서 말했던 Axis-Angle representation에서 말하는 회전 축 벡터인 e가 됩니다. 그리고 회전량 θ가 필요하다고 했습니다. 회전축 벡터 v의 2차 norm값인 ||v||_2 값이 바로 물체의 회전량 θ가 됩니다. 헷갈리겠지만 천천히 생각해보면 다음과 같습니다.

물체의 회전을 표현하는 기존 SO(3) group의 행렬 R이 존재합니다. 이 행렬을 위에서 보였던 Eq(21)을 이용해서 로그화하면 skew-symmetric matrix인 S가 얻어집니다. S의 행렬 성분을 이용해서 구성된 3차원의 v벡터는 기존 회전행렬 R의 회전을 나타내는 회전축이 되고 회전축 벡터의 v의 2차 norm값인 ||v||_2가 기존 회전행렬 R의 회전을 나타낼 수 있는 해당 회전 축을 기준으로하는 회전량(θ)이 됩니다.

우리가 상수값을 로그화하여 변환한 값을 다시 exponential 함수를 취해서 원본값으로 돌려놓을 수 있듯, 로그화된 행렬 S에 다시 exp 연산을 적용하면 원본 행렬인 R로 복원할 수 있습니다. 마찬가지로 단순 행렬 요소에 exponential을 취하는 방법은 아니고 다음과 같이 테일러 급수 비스무리한 공식을 이용해서 표현합니다.

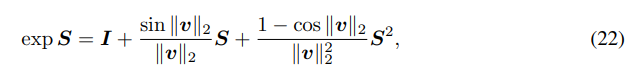
I는 항등행렬입니다. S의 제곱은 S행렬을 두번 행렬 연산한 결과라고 보면 됩니다. 
아무튼 중요한 것은 다음 내용입니다.

물체의 회전을 나타내는 SO(3) group에 속하는 3x3행렬 R을 로그화하면 so(3) group인 S라는 3x3 skew-symmetric matrix로 변환할 수 있다. 이때 S 행렬을 이용하면 Axis-Angle 표현법의 회전축과 회전량을 구할 수 있고 또는 반대로 Axis-Angle 표현법에 따른 회전축과 회전량이 정해져 있다면 행렬 S를 구성할 수 있습니다. 행렬 S는 다시 지수화를 통해 '동일한' 회전을 나타내는 SO(3) group에 속하는 회전행렬 R로 복원하는 것이 가능합니다.

 

실제로 회전행렬 R과 S사이의 변환을 예시를 들어서 따로 설명한 포스팅해두었으니 여기서 예시를 통해 이해하는편이 더 좋을 수 있습니다.

https://biomadscientist.tistory.com/166

SO(3) group 회전 행렬의 so(3) group skew-symmetric matrix 변환

 

포스팅이 너무길어져서 나머지는 (2)에서 추가로 작성하겠습니다.