티스토리 뷰
본 포스팅은 SO(3) group과 so(3) group의 면밀한 대수학, 공학적 개념에 대해서는 따로 다루지 않고 이해를 위해 직관적으로만 이야기합니다. 본인이 애초에 수학이나 로봇공학 전공자가 아니라 완벽하게 이해할 수도 없고 그런 수준의 이해를 요하지 않는 연구를 하고 있기 때문입니다😅
일단은 둘 다 '3차원 공간상의 강체(또는 그냥 물체) 회전을 표현하기 위한 3x3 행렬을 의미한다'고 이해하고 넘어갑시다.
이때 SO(3) group의 행렬을 R이라고 하고 so(3) group의 행렬을 S라고 하겠습니다. 이 둘의 면밀한 차이를 생각하기보다는 저는 다음과 같이 생각하는 편이 이해하기 쉽다고 생각합니다. 굵은 글씨로 표현된 대문자는 행렬을 의미합니다.
숫자에는 서수와 기수가 있죠 하나, 둘, 셋으로 셀 수도 있고 1, 2, 3이라고 표현도 합니다.
셋과 3은 분명 의미는 다르지만 본질적으로 3 또는 셋, 어쨋든 세 개의 추상적인 무언가를 가리킨다는 점에서 본질적으로는 동일합니다. (아주 면밀히 따지자면 완벽하게 맞아떨어지는 개념은 아니라고 생각합니다만)
SO(3) group의 행렬 R과 so(3) group의 행렬 S 역시 이와 같이 생각하면 이해하기 쉬울 것 같습니다.
1. R과 S는 표현은 다르지만 물체의 회전을 나타내는 회전행렬의 서로 다른 종류입니다.
다음으로 SO(3) group와 so(3) group은 그 이름에서도 유추할 수 있다시피 서로 무언가 강하게 연관이 있어보입니다. 지금부터는 R과 S로만 간단하게 말하겠습니다.
행렬에도 로그화/ 지수화 함수를 적용할 수 있습니다. 다만, 우리가 상수에 취하던 로그와 지수와는 조금 다른 개념입니다. 자세한 로그/지수화 방식은 본 포스팅에서는 다루지 않겠습니다만 아래 논문(2022 NIPS, DiffAb)을 발췌하여 간단히 R과 S를 로그화, 지수화하여 상호 변환할 수 있음을 보입니다.

Eq(21)에서 보다시피 행렬 R을 로그화하여 얻어지는 행렬이 바로 행렬 S가 됩니다.
반대로 Eq(22)에서 보다시피 행렬 S를 지수화하여 얻어지는 행렬이 바로 행렬 R이 됩니다.
이렇게 서로 로그/지수화를 통해서 변환된 R과 S는 3차원 유클리디안 공간상에서 물체의 '동일한' 회전을 나타내는 서로 다른 3x3 행렬이 됩니다. 위에서 셋과 3이 서로 동일한 의미를 가진다는 점에서 유사하다고 설명한 이유가 여기에 있습니다. (물론 다시 한번 말하자면 면밀하게 따지면 유사하지 않은 점도 많겠습니다만)
2. R을 로그화하면 S가 얻어집니다. S를 지수화하면 R이 얻어집니다.
3. 얻어진 R과 S는 요소들은 서로 다른 3x3 행렬이지만, 3차원 유클리디안 공간상의 한 벡터에 행렬곱을 진행하면 같은 결과를 얻게됩니다. 다시말해 동일한 회전을 나타내지만 요소들은 서로 다른 두 행렬입니다.
Axis-Angle representation은 물체의 회전을 회전축 벡터e 와 해당 축 방향으로의 회전량 θ를 이용해 나타내는 방법입니다.

위 그림을 보면 지구본이 회전할 수 있는 축이 있고 해당 축을 기준으로 360도 자유롭게 회전할 수 있음을 쉽게 이해할 수 있습니다. 지금 그림상의 지구본은 정해진 축 방향 하나를 기준으로 회전하고 있지만 우리는 머리속에서 지구본의 축을 자유자재로 바꿔볼 수 있습니다. 그 변경된 축을 따라서도 마찬가지로 360도 자유로운 회전이 가능하다는 것도 자명합니다. 머리속에서서 3차원 공간상의 모든 좌표의 어느 방향으로든 축 벡터를 형성할 수 있고, 모든 축을 기준으로 360도 회전을 해봅시다. 이 조합들은 결국 지구본이 회전할 수 있는 모든 3차원 공간상의 회전을 전부 표현할 수 있게 됩니다.
이것이 바로 물체의 회전을 회전축 벡터e와 해당 축에 대한 회전량 θ로 나타내는 Axis-Angle representation 방법입니다.
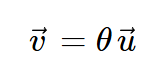
여기서 v벡터가 물체의 회전을 표현하는 3차원 벡터입니다. 이 벡터를 표현하기 위해서 θ라는 회전량 값에 u벡터를 곱해줍니다. 여기서 u 벡터는 위에서 말한 회전축 벡터 e의 normalized된 벡터입니다. Normalization은 단순히 벡터의 norm을 1로 만들어주는 작업입니다. 잘 이해가 안갈 수 있는데 예시를 들어서 설명해보겠습니다.
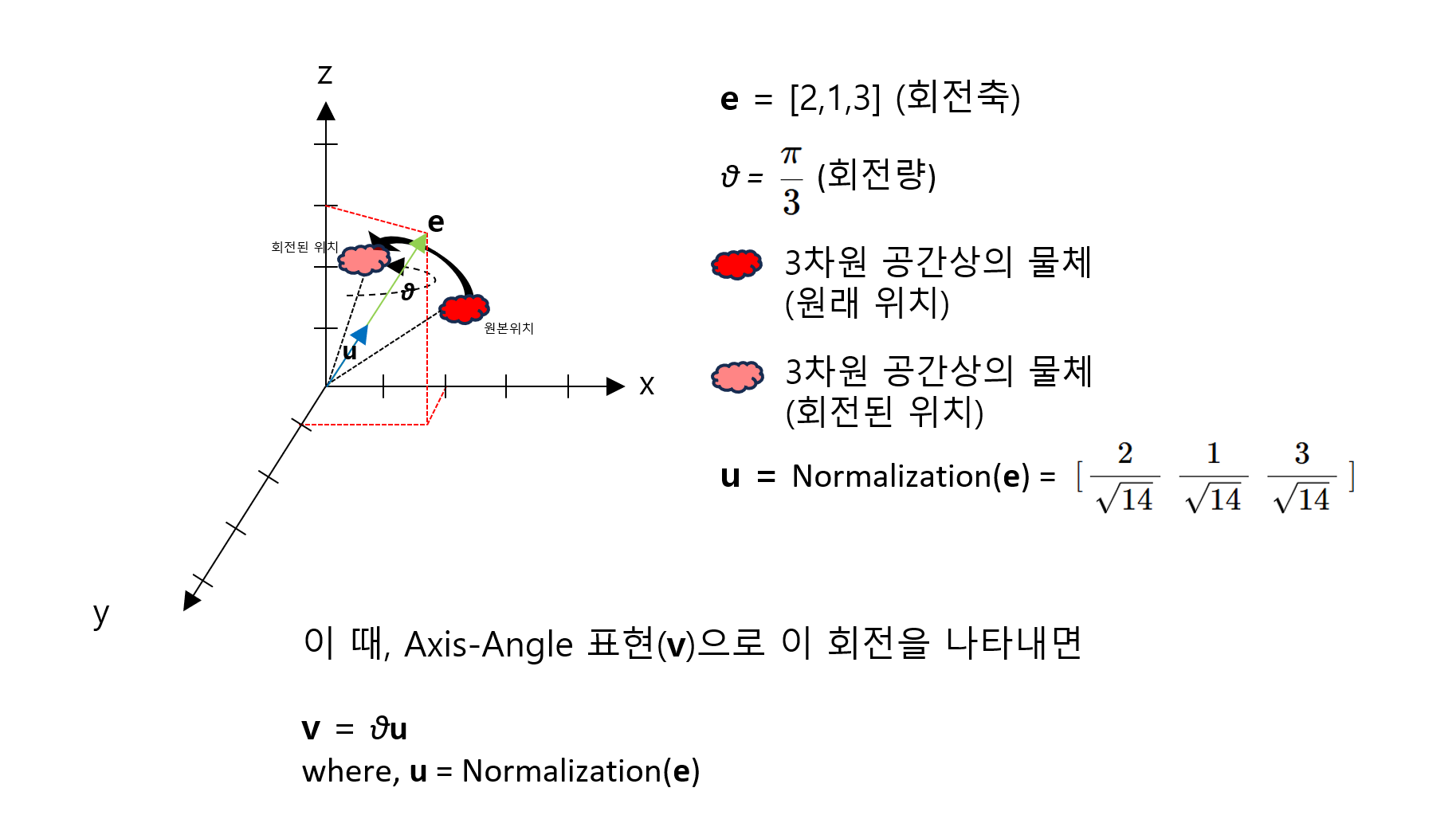
미술에 대한 감각이 제로라 한시간을 끙끙대서 그려보았지만 이게 한계입니다. 공간상의 3차원 벡터로 표현 가능한 회전축e = [2,1,3]을 기준으로 물체의 회전을 나타내는 axis-angle representation 예시입니다.
그냥 찬찬히 그림을 살펴 보시면서 적어둔 모든 값들을 대입해보면 v 벡터를 쉽게 구할 수 있습니다. 애초에 θ와 u 벡터를 모두 구해놓았으니 그냥 곱셈만 해버리면 v 벡터가 얻어집니다. 얻어진 v 벡터가 그림에 나타난 빨간 구름을 회전된 위치로 변환하는데 필요한 회전량과 회전축을 한번에 표현하고 있는 벡터가 됩니다.
갑자기 뜬금없이 이녀석은 왜 설명하였을까요?
Axis-Angle representation으로부터 행렬 S를 유추할 수 있기 때문입니다.
그림에서 우리는 회전축 벡터 e를 normalization하여 u 벡터를 얻었습니다. u 벡터의 각 x,y,z축에 대한 요소를 다음과 같이 표현할 수 있습니다.
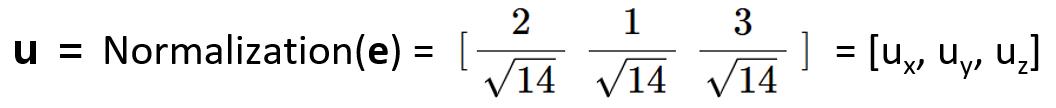
이것으로부터 우리는 so(3) 회전행렬 S를 구성할 수 있습니다. S는 다음과 같이 구성됩니다.
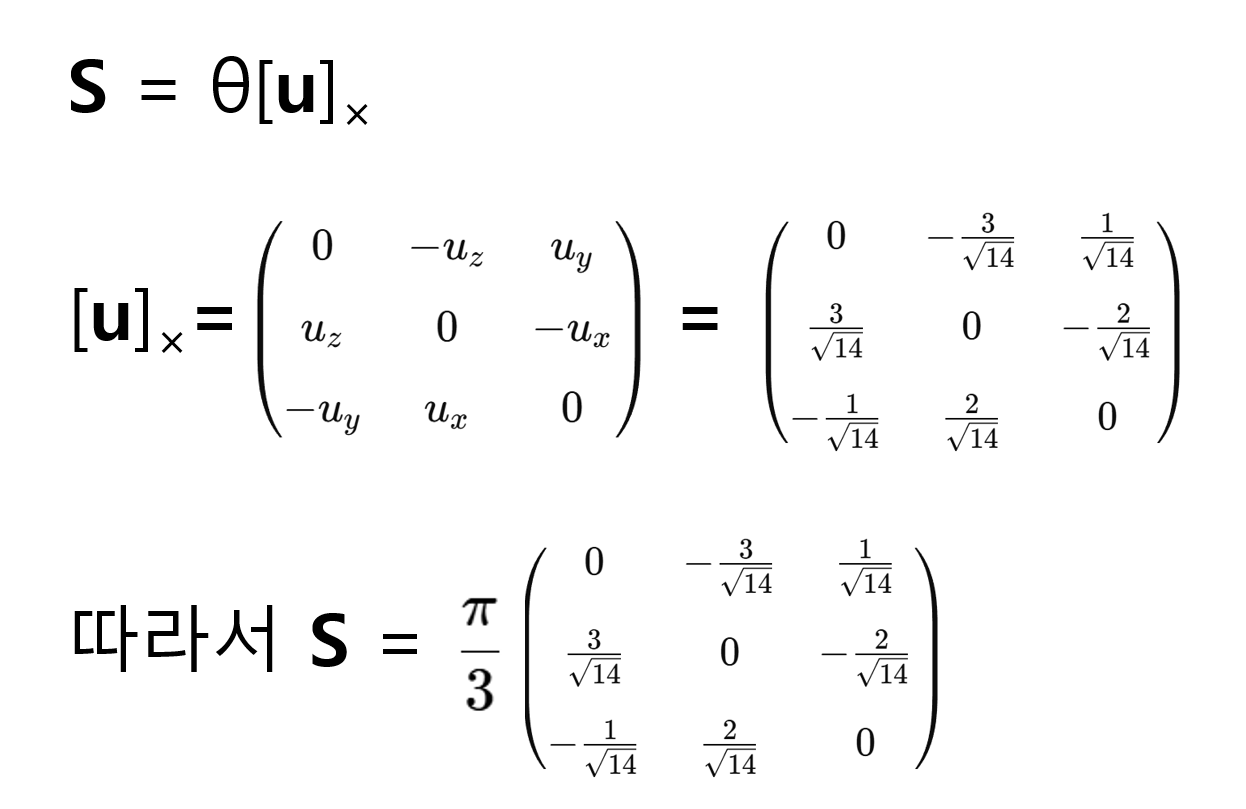
도대체 이 번거로운 짓을 왜 해서 S를 구하려고 하냐면 맨 처음에 우리는 행렬의 지수화를 이용하면 S 행렬을 R 행렬로 변환할 수 있다고 했기 때문입니다. 행렬의 지수화 공식은 다음과 같습니다.

여기의 v 벡터는 위에서 말한 것 처럼 θ와 u 벡터를 단순 곱셈하면 됩니다. v의 norm을 구하는 것은 어렵지 않습니다.
따라서 단위행렬 I와 so(3) 회전행렬 S, v벡터 모두 구했기 때문에 지수화된 S 행렬 exp(S)를 구하는 것은 식은 죽 먹기입니다. 이 계산 결과로 구해진 행렬이 바로 SO(3) group인 R 행렬이 됩니다.
4. Axis-Angle 표현법을 사용해 물체의 회전을 S 행렬로 표현할 수 있습니다.
5. S 행렬은 위에서 말한 것 처럼 지수화를 통해 R 행렬로 변환할 수 있습니다.
6. 우리는 오일러 각대신 Axis-Angle 표현법을 이용해 물체의 회전을 표현하는 것이 이상적임을 입증하였습니다.
제가 생각했을 때 가장 중요한 사실은 다음과 같습니다.
R행렬과 exp(S)행렬을 이용해 물체를 회전한 결과가 완전히 동일하다는 것입니다.


이상으로 SO(3)와 so(3) group의 회전행렬의 변환에 대해 공부했습니다.
마지막 질문 : 단백질 생성모델 연구자 입장에서 이 번거로운 것을 왜 공부해야하느냐?
간단하게 말하자면 아미노산의 R group의 회전 방향인 orientation을 diffusion 시키기 위해서는 SO(3) group이 아닌 so(3) group을 이용해서 먼저 diffusion 한 뒤, SO(3) group으로 변환하는 방식을 사용해야하기 때문입니다.
'Background > Math' 카테고리의 다른 글
- Total
- Today
- Yesterday
- 3b1b
- 3B1B따라잡기
- 오일석기계학습
- 파이썬
- MorganCircularfingerprint
- MLE
- manim
- 이왜안
- 선형대수
- 기계학습
- antigen antibody interaction prediction
- eigenvalue
- MatrixAlgebra
- 최대우도추정
- 백준
- 나노바디
- 논문리뷰
- Manimlibrary
- dataloader
- 인공지능
- manimtutorial
- nanobody
- manim library
- elementry matrix
- eigenvector
- ai신약개발
- 베이즈정리
- marginal likelihood
- Matrix algebra
- 항원항체결합예측모델
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
