티스토리 뷰
VAEs 이해를 위한 배경지식 (2) Variational Inference(VI) and Evidence Lower BOund (ELBO)
벼랑끝과학자 2024. 2. 13. 23:19https://biomadscientist.tistory.com/141
VAEs 이해를 위한 배경지식 (1) Markov Chain Monte Carlo(MCMC) 마코프체인-몬테카를로
Markov Chain https://www.youtube.com/watch?v=i3AkTO9HLXo https://www.youtube.com/watch?v=yApmR-c_hKU https://www.youtube.com/watch?v=5QAfQZjCrRM Stationary Distribution(Stationary States) https://www.youtube.com/watch?v=4sXiCxZDrTU 2024년부터는 생성
biomadscientist.tistory.com
지난 번 포스팅에서는 VAEs를 이해하기 위한 배경지식의 첫번째로 Markov Chain Monte Carlo(MCMC) 방법에 대해 다뤘다. 이번 포스팅에서는 Variational Inference(이하 VI)와 ELBO에 대해 다루려 한다. VAEs를 공부하면서 답답했던 것은 도대체 이놈의 Variational Inference가 무엇인지 명확한 개념을 파악하지 못하는 것이었다.
이번 포스팅에서는 VAEs에서의 VI의 개념이 무엇인지 다뤄보고 Optimal surrogate distribution을 찾기 위한 Loss term이 되는 KL Divergence와 ELBO에 대해 이해해 보기로 하자.
모든 포스팅은 다음 유튜버의 VI관련 영상들을 참고하여 작성되었고 VI에 대해 이분만큼 이해하기 쉽게 정리해준 영상이 없는 것 같으니 포스팅도 좋지만 VAEs를 공부하는 사람이라면 반드시 아래 영상들을 보는 것이 좋겠다.
- https://www.youtube.com/watch?v=HxQ94L8n0vU&list=PLISXH-iEM4JloWnKysIEPPysGVg4v3PaP
- https://www.youtube.com/watch?v=gV1NWMiiAEI
- https://www.youtube.com/watch?v=u4BJdBCDR9w
Posterior가 도대체 뭐야?
먼저 우리가 찾고자 하는 Posterior P(Z|X=D)의 의미가 무엇인지를 예시를 들어 이해해보자. 예를들어 컴퓨터가 다양한 사진(D)을 학습한다. 사진에 나타나는 주된 특징을 살펴보자. 어떤 배경을 갖고 있는지, 주로 인물이 찍혀있는지 동물이 찍혀있는지, 채도는 어떤지, 색온도는 어떤지, 밝기는 어떤지 등의 다양한 정보들이 숨어있을 것이다. 이렇게 주어진 데이터속에 내포된 정보들을 latent variable(Z)라고 이야기한다.
그렇다면 사후확률 P(Z|D)의 의미는 무엇일까? 데이터 D를 관찰했을때 특정한 latent variable Z가 나타날 확률(Probability)을 의미한다. 직관적으로 설명하자면 당신앞에 100장의 사진(D)이 있다. 그 중 90장은 강을 배경으로하는 사람들이 찍혀있는 사진이었고, 나머지 10장은 산에서 찍힌 동물의 사진이다. 이제 101번째 나올법한 가장 높은 가능성을 가질만한 사진을 그려보라고 하자. 당신은 강가의 사람을 그릴까? 아니면 산에서 찍힌 동물을 그릴까? 그것도 아니라면 자동차 그림을 그릴까? 뭣도 아니라면 피카소의 우는 여인을 그려서 준다해도 할 말은 없겠다.
과연 당신이 그리려 했던 네가지 후보 P(Zriver|D), P(Zmountain|D), P(Zcar|D), P(Zpicasso|D)중 과연 어떤 것이 가장 높은 가능성을 가질까? 만약 여기서 P(Zriver|D)가 아니라 다른 것이 더 높은 가능성을 가질 것 같다고 생각했다면 돌아가서 다시 조건부 확률 개념부터 공부하는 것이 좋겠다.
그러나, 생각해보자. 세상에 그릴 수 있는 그림은 한가지인가? 지금 내가 나타낸 latent variable Z에는 오직 그리려는 물체 하나만 특징으로(1차원으로) 나타나고 있다. 그리고 그마저도 세상의 물체는 한두가지인가? 단순한 1차원의 latent variable Z만을 이용한다고 하더라도 찾아야 하는 Z의 범주는 엄청나게 많다 (Continuous latent variable Z). 게다가 실생활에서 latent variable Z는 보통 한가지는 커녕 수십, 수백가지도 될 수 있다. 똑같은 강을 그리더라도, 강의 폭, 강의 물살의 세기, 강 주변은 모래인지 돌인지, 날씨는 흐린지 맑은지 등 이야기하자면 끝도없는 latent variable을 이야기 할 수 있겠다. 수학적으로 말하자면 latene variable Z는 1차원이 아니라 수십, 수백차원의 continuous variable로 이뤄진 벡터라는 것이다.
결국 우리가 찾고자 하는 Posterior P(Z|D)는 '주어진 데이터를 이용했을 때, 특정한 latent variable Z가 나타날 확률분포'가 된다. 보통 Posterior P(Z|D)는 명확한 closed form (수식으로 명시가능한 함수)을 찾는 것이 불가능한데, 위에서 설명한 내용을 참고하면 이해가 될 것이다. 아주 단순한 1차원으로만 생각해도 세상에 존재하는 그 모든 물체들 중 어떤것을 어떤 확률로 그릴지 전부 알 수 있는가? 오직 신만이 알고 있겠지.

위 그림을 살펴보자, 파란색으로 나타낸 그래프는 우리가 찾고자 하는 Posterior distribution P(Z|D)이다. 아주 아주 단순한 문제가 아니면 그림조차 그릴 수 없기에 (사실 이 그래프를 그린 것 조차 오류이다. 명확한 P(Z|D)는 절대로 알 수 없다.), latent variable Z는 1차원일때를 가정했다. 주어진 데이터를 이용해서 latent variable Z의 probability를 모두 나타낼 수 있다면 우리는 P(Z|D)를 이용해서 다음에 나올법한 그림들을 얼마든지 그려낼 수 있다. 단순히 확률을 따라서 샘플링만 하면 되니까.
그런게 가능했다면 생성모델을 만드는 일 따위는 전혀 어렵지 않았겠지. 지금부터 왜 Posterior는 구할 수 없는 것인지, 구할 수 없다면 어떻게 이 문제를 bypass할 것인지? 이 두가지 문제에 집중해서 긴 이야기를 시작해 보려한다.
Posterior를 구할 수 없는 이유

Directed Graphical Model(DGM)이 있다. 관찰된 데이터 D와 latent Z를 갖는다고 하자. 예를들어 위에서 언급했던 것 처럼 m개의 픽셀을 갖는 이미지를 D로, 그 이미지를 나타낼 수 있는 가장 강한 n개의 특징을 latent Z라고 생각하면 된다.
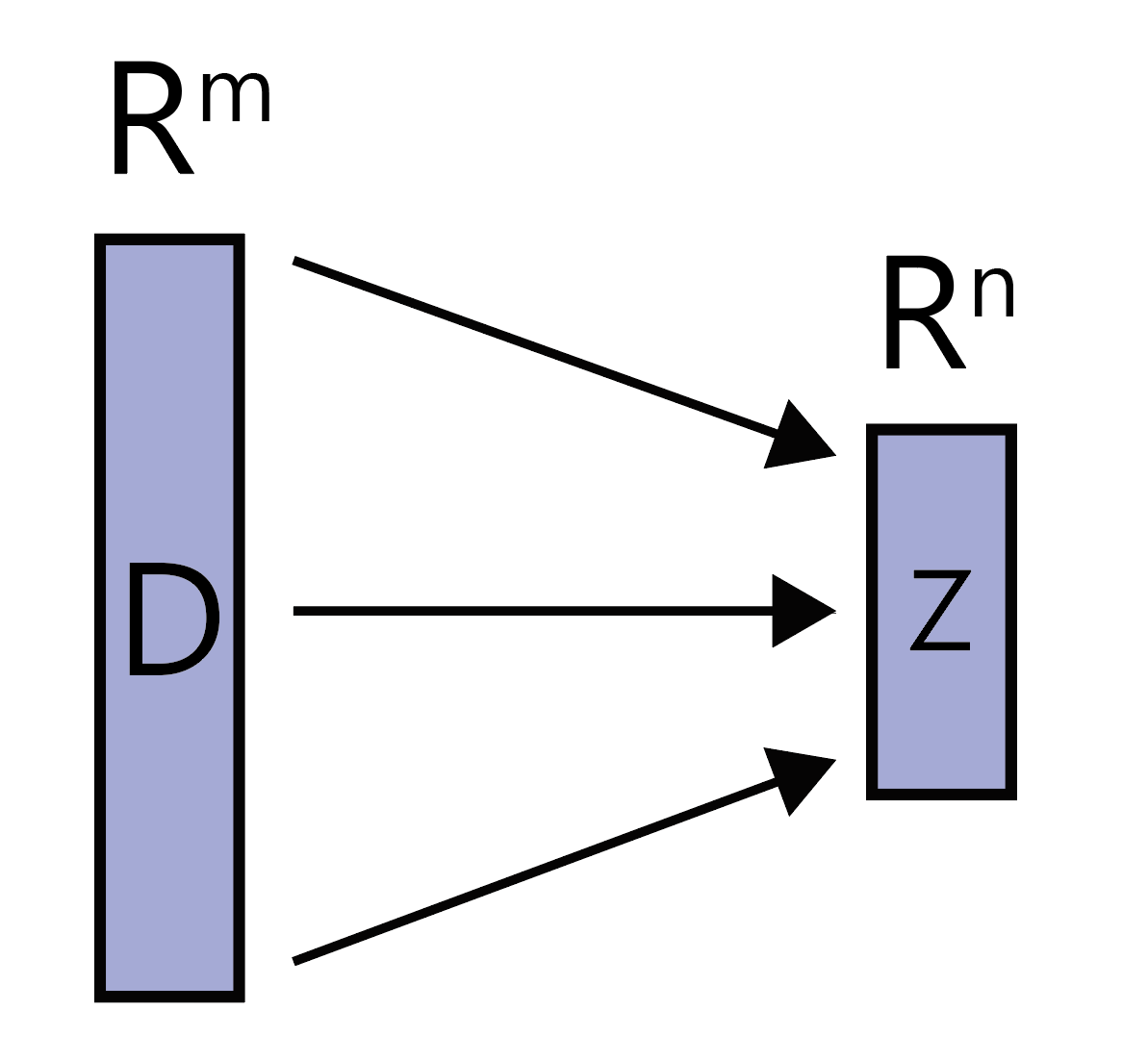
이 경우 우리는 Joint Probability P(Z,D)를 알고 있는 것이다. (P(Z|D)를 알고 있는 것이 아니다.) 이제부터 D로부터 Z의 정보를 알아내어 Posterior P(Z|D)를 찾아보려 한다. 이렇게 '어떤 정보를 이용하여 또다른 정보를 추론해내는 과정'이 들어가면 머신러닝이나 딥러닝 분야에서 'Inference'라는 용어를 사용한다. Variational Inference에서 "Inference"라는 용어가 등장하는 이유는 여기에 있었다.
본론으로 돌아와서 베이즈 룰을 참고하면 다음과 같은 식을 얻을 수 있다. 만약 아래 식을 이해할 수 없다면 아직 VAEs를 공부하기엔 어렵다고 생각되니 베이즈 룰, 조건부 확률, 결합확률, Marginal distribution, Marginalization 개념을 먼저 공부하고 오는 것이 좋겠다.

위에서 Joint probability P(Z,D)는 우리가 접근 가능한 값이라고 하였다. 다시말하면 Likelihood와 Prior는 우리가 알 수 있다는 것이다. 그런데 Evidence 또는 Marginal값은? (지금부터는 Evidence로 통일하겠다.) P(D)를 구하기 위해서는 Joint distribution인 P(Z,D)에서 Z를 marginal out시켜야 한다. Z는 continuous variable이므로 다음과 같은 식이 되겠다.
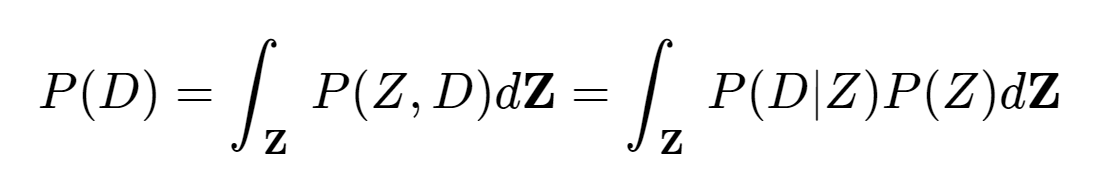
Z를 대문자에 볼드체로 작성한 것을 집중하자 Latene Variable Z는 1차원이 아니다. 벡터다 이게 무슨 말이냐면...
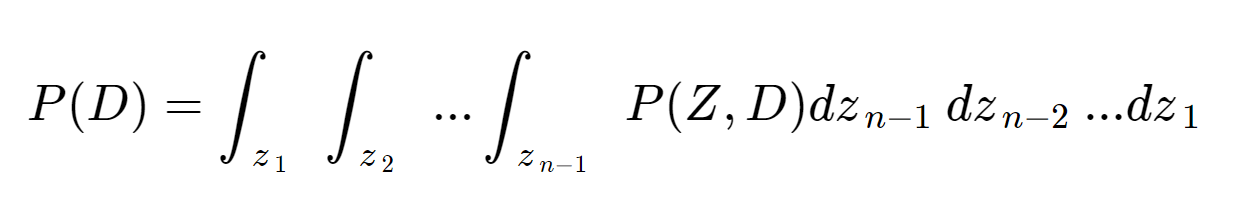
이런 끔찍한 n중 적분을 해야 한다는 말이 된다. 컴퓨터라면 가능하지 않냐고? 사실 정확하게는 모르겠지만, 이건 컴퓨터 입장도 들어봐야 한다. 불가능에 가까울 정도로 시간이 엄청나게 많이 소요되는 작업이라고 한다. 따라서, 여기서 문제가 발생했다. Evidence인 P(D)를 명확하게 구할 수 없다. 그러면 식1. 베이즈 룰에 돌아가서 보면 Posterior도 자연스럽게 구할 수 없다. 우항의 모든 값을 알지 못하면 좌항도 완성되지 않는것은 너무나 자명하다. 다시 맨 처음 봤던 그림1 을 살펴보자

파란색 그래프 P(Z|D)는 그릴 수 없다는 이유가 이제는 이해가 되어야 된다. 완성할 수 없는 함수를 이용해 그래프를 그린다? 있을 수 없다. 자, Posterior는 못구한댄다. 포기하자. 라고 생각했다면 컴퓨터 공학자, 수학자들은 손가락만 빨고 있었겠다. 항상 우리는 이렇게 명확히 구할 수 없는 무언가에 대해 approximation을 통해서 문제를 해결해왔다.
Remedy! (1) surrogate distribution을 이용하자!
전략 : Posterior Distribution인 P(Z|D)를 가장 잘 approximation하는(==Optimization) surrogate distribution q(z)를 찾자.
자, 여기서 "Variational" 용어의 등장 이유가 나온다. Variational calculus라는 수학 분야가 있는데 이 분야는 '임의 함수에 대하여 최적값을 찾는" 분야를 의미한다. q(z)는 함수다. 그리고 우리는 optimization을 통해서 P(Z|D)를 가장 잘 approximation하는 q(z)로 최적화하려 한다. 따라서 이 방식은 variational calculus와도 궤를 같이한다. 이런 관점에서 "Variational Inference"의 "Variational"이라는 용어가 등장하게 된 것이다. 비로소 그놈의 변분 추론이라는 해괴망측한 한국말이 무엇인지 이해하게 되었다. https://en.wikipedia.org/wiki/Calculus_of_variations참고
각설하고, 위에서 말한 P(Z|D)를 가장 잘 approximation하는 q(z)는 다음과 같이 나타낼 수 있겠다. q(z) ≈ P(Z∣D)
딥러닝 분야에서 함수를 optimization하는 과정은 보통 어떻게 진행되는가? Loss function을 이용한 backpropagation으로 parameter를 Gradient Discent를 이용해 업데이트하는 방식이 가장 널리 이용되고 있다. 우리도 똑같이 이런 과정을 통해서 최적의 q*(z)를 찾아갈 것이다. 이때 가장 유용한 loss term으로 사용될 수 있을만한 것은 무엇이 있을까? 여기서 바로 KL-Divergence(이하 KLD)가 등장한다.
자! KLD는 여기서는 일단 Probability distribution을 나타내는 Probability Density Function(PDF)간의 거리(유사도)를 재는 척도라고 생각하면 되겠다. 다만! KLD는 명확하게 Distance의 모든 property를 만족하지는 못하기 때문에 Distance라고 이야기해서는 안된다. KL-Distance가 아니라 Divergence인 이유는 여기에 있다. 한가지 예를 들자면 KLD(q || p) =! KLD(p || q)이다. 만약 거리개념이었다면 a와 b사이의 거리는 당연히 b와 a사이의 거리와 같아야 한다. 우리가 알아야 하는 KLD의 특성은 다음과 같다.
- 두 Distribution이 완전히 같은 경우 KLD=0
- 두 Distribution이 다르면 다를수록 KLD값은 증가한다. [0, ∞)
- 따라서 KLD값은 반드시 0 이상이다.
이는 나중에 ELBO를 설명할 때 중요한 개념이니 꼭 기억하도록 하자.
다시 q(z) ≈ P(Z∣D)로 돌아와 볼까? 그럼 우리의 목적은 q(z)와 P(Z∣D) 사이의 KLD값을 최소화 하는 것이다. 이를 수학적으로 나타내면 다음과 같다.
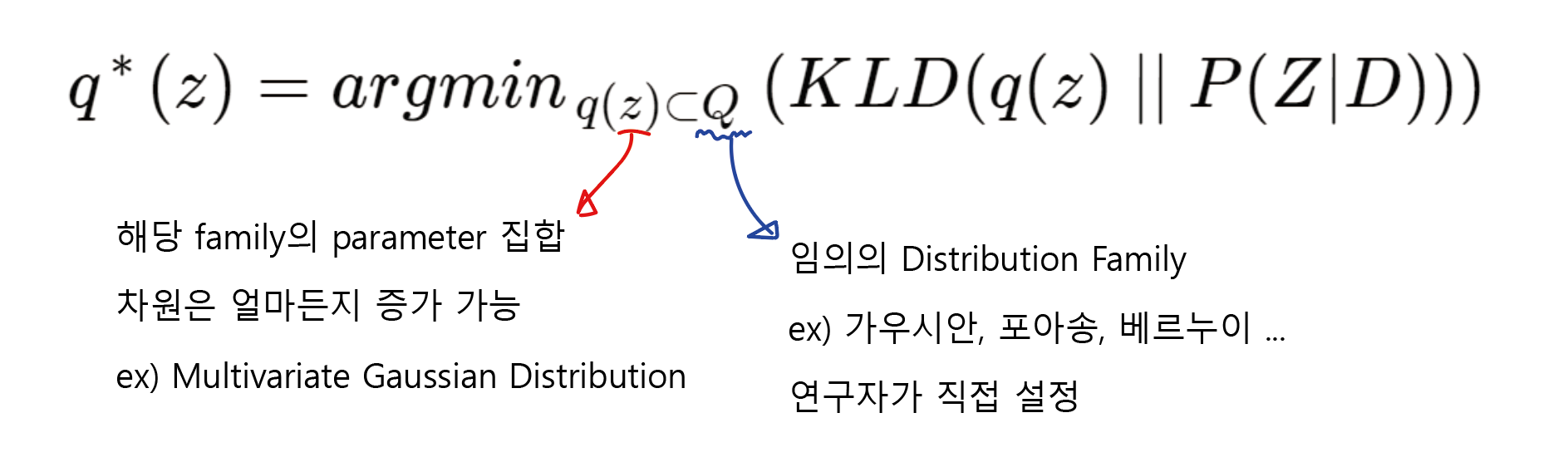
다시말해 Posterior Distribution P(Z|D)와 KLD값이 최소가 되도록 하는 최적의 surrogation distribution q*(z)를 찾겠다는 것인데, 이때 q(z)는 simple parameter를 가지는 명확한 closed form이 구성되어 있는 distribution을 사용한다. 아주 대표적인 것이 평균과 분산을 파라미터로 가지는 가우시안 분포가 있겠고 실제로 VAEs에서는 이 가우시안 분포를 q(z)로 사용한다. 물론 연구자에 따라 가우시안이 아니라 다른 분포를 사용할 수도 있다.
이럴수가, 이제 그럼 q(z)와 P(Z|D)를 이용해 KLD를 계산만 해주고 loss를 이용해서 backpropagation하면 되겠군! KLD의 공식은 다음과 같다.
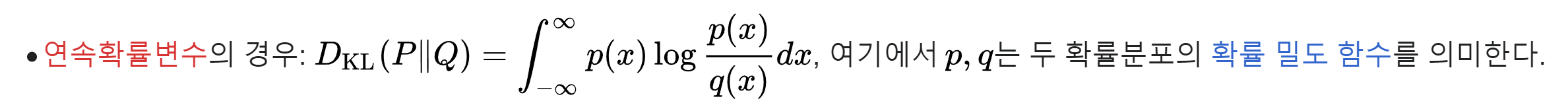
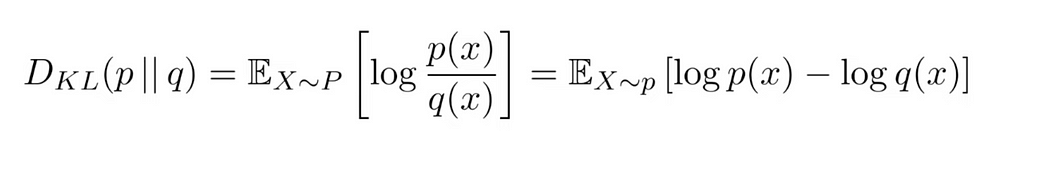
이제 KLD를 우리 문제에 맞게 q(z)와 P(Z|D)에 적용해보면 다음과 같은 식이 된다.

그런데 여기도 보면 Posterior distribution인 P(Z|D)가 KLD term에 들어있는 것을 볼 수있다. 어라 이러면 q(z)를 이용해 KLD를 써서 근사시킨다는 근사한 remedy가 아무런 의미가 없어진게 아닌가? 맞다. 이 방법으론 여전히 posterior distribution때문에 q(z)와 P(Z|D) 사이의 KLD를 구할 수 없다. 당연히 P(Z|D)가 뭔지 모르는데 KLD를 어떻게 구할까. 따라서 우리는 두번째 우회 방법을 사용해야 한다.
Remedy! (2) Rearrange to compute something!

우리가 구해야 하는 KLD값은 다음 식과 같다. 그러나 P(Z|D)는 Posterior Distribution으로 직접 구할 수 없다. 그렇다면 어떻게 해야할까? 직접 구하지 못하는 Posterior를 다른 형태로 치환해서 문제를 접근해보자. 식1.에서 언급한 Baye's Rule을 다시한번 살펴보자 이를 이용하면 Posterior P(Z|D)를 다음과 같이 나타낼 수 있다.

이것을 식7에 대입하면 다음과 같다.
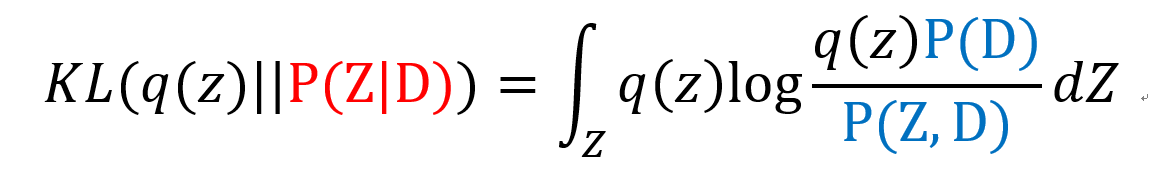
로그의 성질에 의해 다음과 같이 두 항으로 나눌 수 있다.
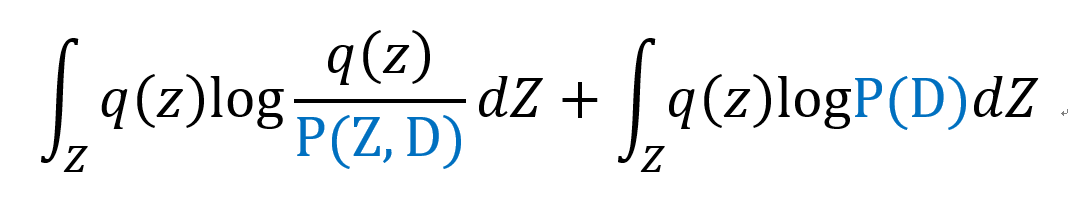
적분으로 나타낸 식을 다시 Expectation notation으로 바꿔서 나타내면
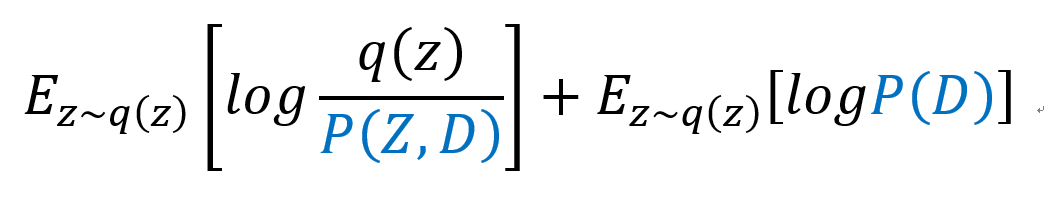
이때 우항의 logP(D)는 Random Variable Z와 무관한 상수값이므로 Expectation을 제거할 수 있고, 좌항은 로그성질에 의해 음수로 바꿔 준 뒤, 분자와 분모의 순서를 바꿔줄 수 있다.
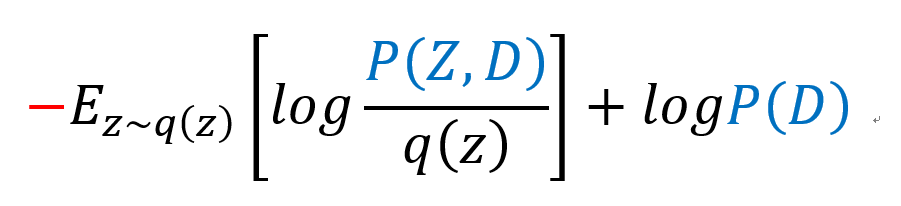
이제 좌항의 음수를 제외한 나머지 Expectation value 값은 surrogate distribution q(z)에 dependent이므로 L(q)라고 치환해보자.
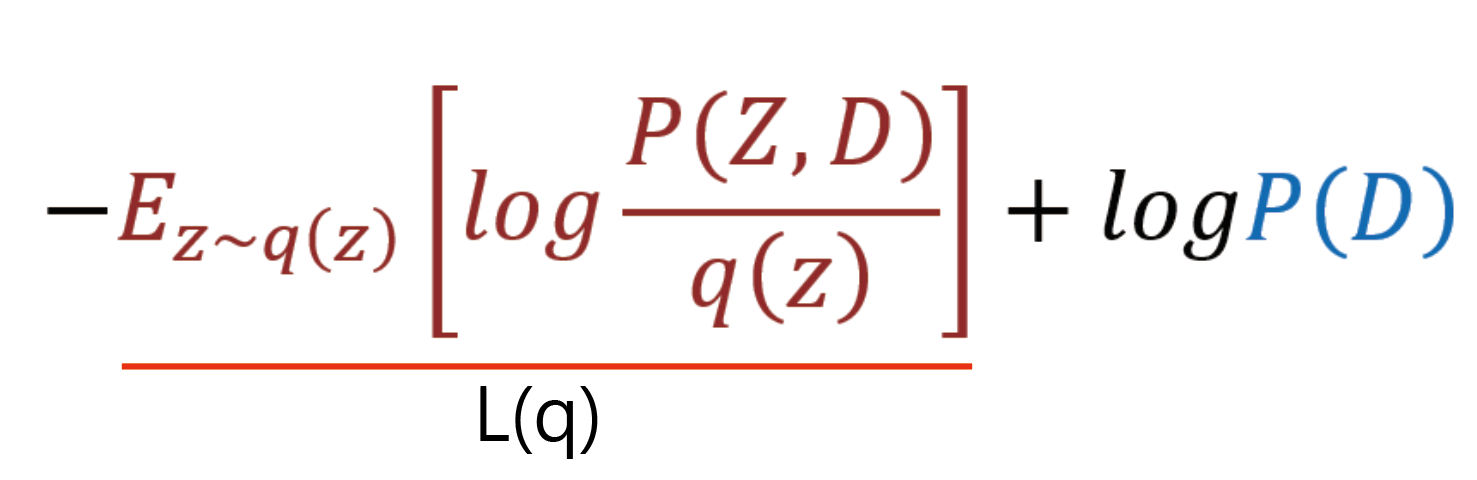
이제 최종적으로 남은 식만 정리해보면 다음과 같다.
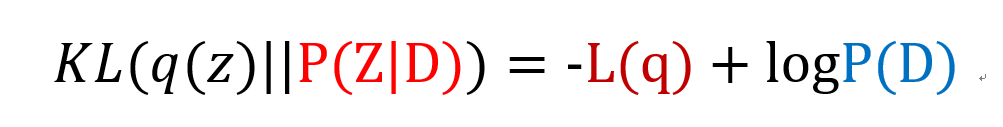
Evidence Lower BOund (ELBO)
정신을 바짝 차리자, 이제 VAEs에서 가장 중요한 개념인 ELBO에 대해 설명하려한다. 이부분을 이해 못하면 말짱 꽝이다.
자 이제 생각해보자, P(D)는 joint distribution P(Z,D)에서 Z를 margianl out시킨 Evidence로 어찌되었든 결국 확률 분포인 P의 공리를 만족시키기 위해서 그 값은 반드시 0~1 사이여야 한다. 그럼 이제 0~1 사이 값에 log를 취한 logP(D)의 값은 어떻게 되는가? 먼저 로그함수의 그래프에서 0~1 사이의 값을 살펴보자
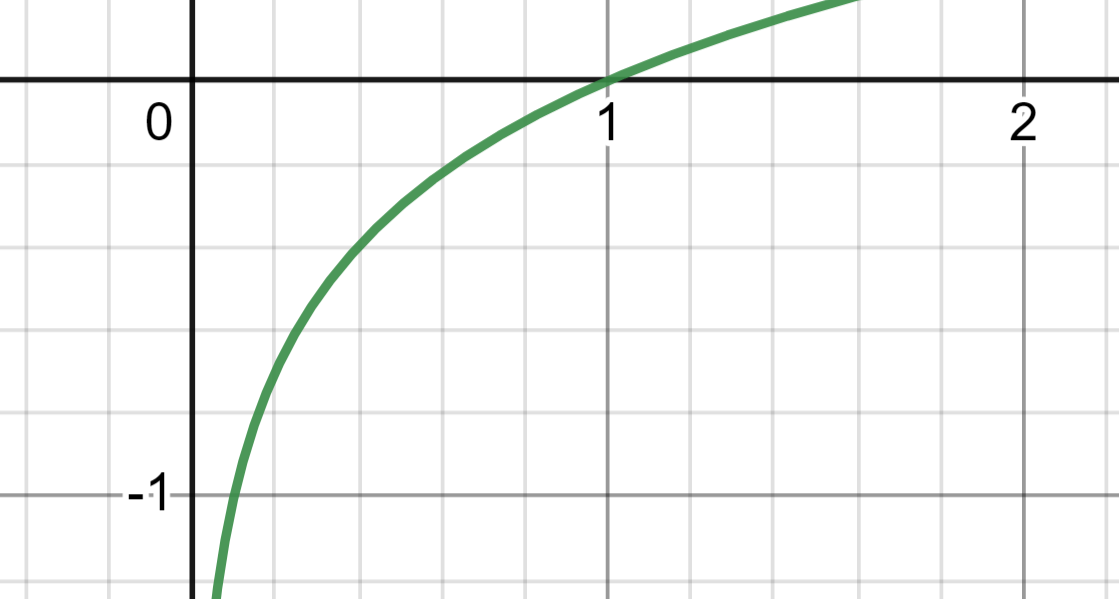
log(x) where 0 <= x <=1의 범위는 (-∞, 0] 임을 볼 수 있다. 이를 감안하면 logP(D)는 사실상 항상 음수값이라고 정의할 수 있다. 자 이제 다시한번 식14. 최종식을 살펴보자
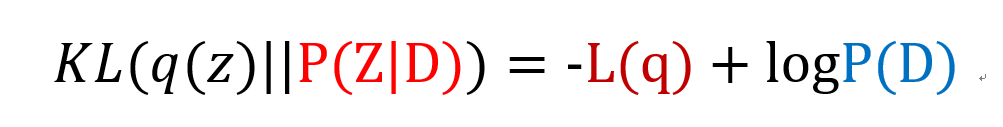
좌항의 KLD값은 음수가 될 수 있는가? 거리의 개념을 완전히 만족하지는 못하지만 KLD값은 최소가 0으로 반드시 양수값이다. 우항의 logP(D)는 항상 음수라고 했다. 그러면 다음과 같은 느낌이 된다.
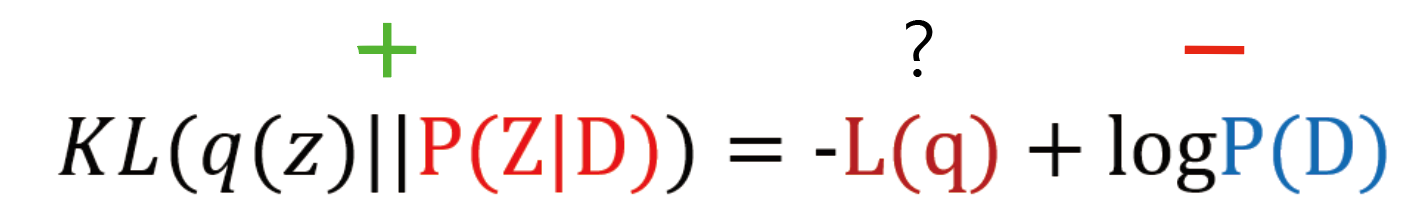
자, 이제 -L(q)는 음수여야 하는가 양수여야 하는가? 그렇다면 L(q)는 음수여야 하는가 양수여야 하는가? 자명하지만 L(q)는 반드시 음수여야만 하고 그 값은 logP(D)보다 반드시 작아야만 한다. 그렇지 않은 경우에는 좌항의 KLD값을 양수로 만들 수 없다.
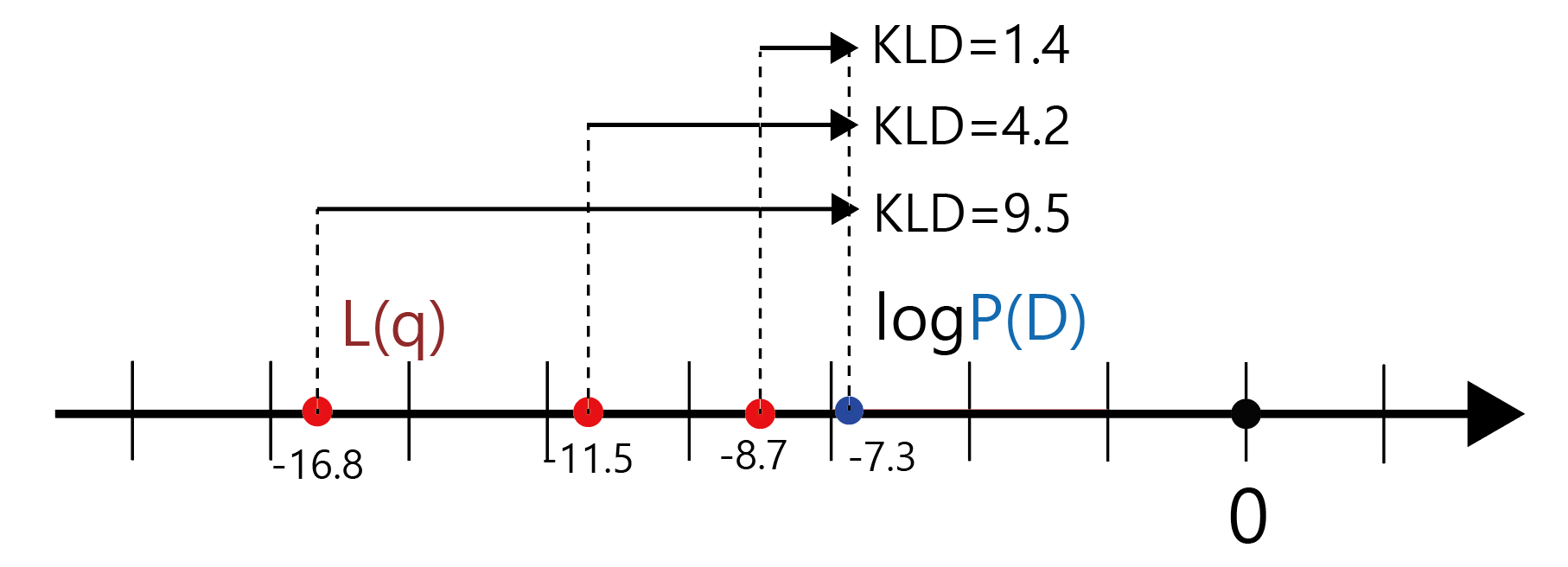
쉬운 이해를 위해서 logP(D)값이 임의로 -7.3이라는 값을 가졌다고 해보자. L(q)는 -16.8이라는 값을 가졌다고 해보자
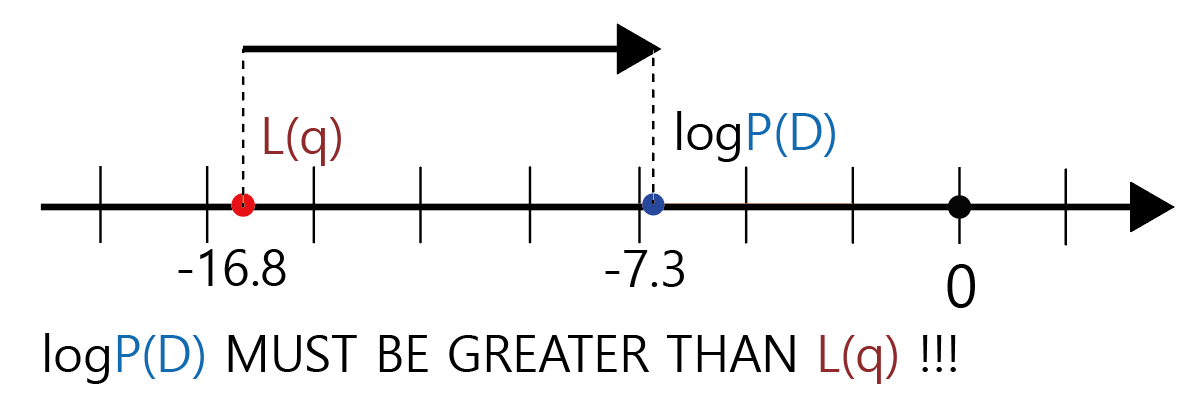
그림3.을 차근히 살펴보면 KLD 값이 양수가 되기 위해서는 L(q)가 반드시 Evidence인 logP(D)보다 작아야 한다는 사실을 이해할 수 있을 것이다. 그 말은 반대로 Evidence인 logP(D)는 반드시 L(q)보다는 커야한다는 말이라는 것도 이해할 수 있을 것이다. 그럼 마지막으로 L(q)가 Evidence Lower BOund (ELBO)가 된다는 사실도 이해할 수 있을 것이다.
자, 정말 마지막으로 생각해보자 KLD값이 점점 작아진다는 말은 무엇을 의미하는가? Surrogate distribution q(z)와 Posterior distribution P(Z|D)의 유사도가 점점 가까워짐을 의미한다.
KLD값이 점점 작아지려면 ELBO와 Evidence의 관계는 어떻게 되어야 하는가? ELBO가 Evidence쪽으로 점점 가까워지면 가까워질 수록 KLD값은 점점 작아진다. 다시말해 ELBO값이 커지면 커질수록, Surrogate distribution q(z)와 Posterior Distribution P(Z|D)의 거리가 가까워지고, 잘 Approximation 된 q(z)가 얻어진다는 것을 의미한다.
그러면 이제 우리는 문제를 다음과 같이 정의할 수 있게되었다.
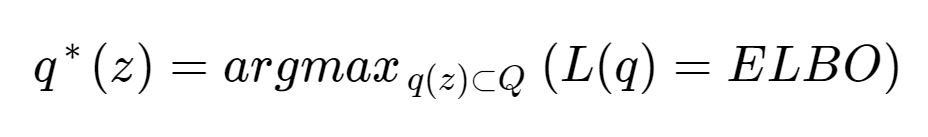
이상으로 VI와 ELBO에 대한 개념에 대해서 정리해 보았다. 나는 공부하면서 이제서야 조금이나마 VI가 무엇인지, ELBO가 무엇이었는지 이해하게 되었다. 그러나 여기에 나온 수식은 surrogate distribution의 parameter optimzation 부분은 생략하고 이해하기 쉽도록 한 notation이고 실제 VAEs 논문을 보면 그 수식이 같은 말을 하고 있음에도 훨씬 어려운 notation을 사용하기 때문에 이해하기가 상당히 까다롭다. 다음 포스팅에서는 VAEs에서 실질적으로 어떻게 ELBO등을 적용해 Surrogate distribution을 찾는 것인지, surrogate distribution의 parameter들은 또 어떻게 optimization한다는 것인지를 조금 더 자세히 살펴보려 한다.
'Background > Math' 카테고리의 다른 글
| SO(3) group 회전 행렬의 so(3) group skew-symmetric matrix 변환 (0) | 2025.03.31 |
|---|---|
| understanding diffusion models: a unified perspective "equation 43~45" 유도과정 (2) | 2024.04.16 |
| VAEs 이해를 위한 배경지식 (1) Markov Chain Monte Carlo(MCMC) 마코프체인-몬테카를로 (2) | 2024.02.07 |
| Jacobi iteration method (야코비 반복법) (0) | 2024.02.02 |
| Cauchy Sequences/completeness/complete metric space 코시 시퀀스와 완비성, 완비거리공간 (0) | 2024.01.31 |
- Total
- Today
- Yesterday
- Manimlibrary
- 나노바디
- elementry matrix
- 베이즈정리
- 항원항체결합예측모델
- 기계학습
- 3B1B따라잡기
- 최대우도추정
- 오일석기계학습
- 선형대수
- antigen antibody interaction prediction
- MatrixAlgebra
- manimtutorial
- 인공지능
- ai신약개발
- eigenvalue
- eigenvector
- manim
- marginal likelihood
- Matrix algebra
- dataloader
- nanobody
- 이왜안
- 파이썬
- 백준
- MorganCircularfingerprint
- manim library
- MLE
- 논문리뷰
- 3b1b
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
