티스토리 뷰
VAEs 이해를 위한 배경지식 (1) Markov Chain Monte Carlo(MCMC) 마코프체인-몬테카를로
벼랑끝과학자 2024. 2. 7. 18:56Markov Chain
- https://www.youtube.com/watch?v=i3AkTO9HLXo
- https://www.youtube.com/watch?v=yApmR-c_hKU
- https://www.youtube.com/watch?v=5QAfQZjCrRM
Stationary Distribution(Stationary States)
2024년부터는 생성모델에 대한 연구를 하기 위해서 Generative model의 할애비뻘 된다 할 수 있는 VAEs 논문부터 시작해서 아버지뻘 되는 Diffusion과 아들뻘되는 DDPM 논문까지 빠르게 공부하고 생성모델 연구로 뛰어드는 한 해가 되려 한다. 나는 객관적으로, 주관적으로 봐도 수학에 대한 이해도가 상당히 떨어지지만 그래도 최선을 다해볼 생각이다.
그러기 위해서는 당연히 VAEs 모델에 대한 이해가 있어야겠고, 지금까지 처럼 대충 'VAEs는 인코더로 latent vector Z의 평균과 분산 학습하고, 그것을 reparameterization trick을 사용해 vector로 복원(샘플링)하여 디코더를 이용해 복원한다' 라는 식의 수박 겉핥기 지식으로는 절대 안된다고 생각한다.
그 첫번째 시간으로 지금까지 이해하기 워낙 어려워서 계속 도망치기만 했던 MCMC에 대한 이해를 해보자. 이후로 Variational Inference(VI)에 대한 포스팅을 예정하고 있다.
MCMC는 무엇이며 왜 사용하는가?
일단 문제 해결에 컴퓨터를 사용하는 이유가 무엇일까? 컴퓨터로 우리는 무엇을 풀려고 하는 것일까? 우리가 컴퓨터로 문제를 해결하는 방식은 무엇인가? 확실하지 않지만 내가 생각하는 직관적인 이해는 이렇다. (당연히 틀렸을 수 있다.)
- 실생활의 모든 문제는 각각의 Target distribution을 가질 것이다. 그 Target distribution을 명확히 알 수 있다면 다음 발생할 현상에 대한 명확한 예측이 가능하다 ex) 주식가격 예측, 산불 발생 예측, 시험 등수 예측 등등
- 그러나 그 문제의 Target distribution은 오직 신만이 알 수 있다.
- 인간은 그 문제를 approximation하는 최적의 distribution을 찾아야한다.
- 그 approximated distribution을 찾는 방법론은 크게 두 가지로 다음과 같다.
- 주어진 데이터를 이용해 명확한 model을 만들어 최적의 함수를 찾는 방식 (parametric method)
- MLE, MAP, Variational Inference(VI)같이 loss function의 optimization을 이용하는 방법
- 샘플링을 통한 최적화 (Baysian Inference(BI) 예를들어 Rejection sampling, MCMC를 이용한 방법 등)
- model을 가정하지 않고 simulation/sampling을 통해 해당 분포의 데이터를 무한히 많이 얻어 distribution을 근사시키는 방식 (non-parametric method 예를들어 Kernel Estimation, K-Nearest Neighbors )
MCMC 이전에도 많은 연구자들이 sampling을 통한 distribution을 얻기 위한 방법을 생각했었고, 그 전까지 Accept-Reject sampling이라는 기법을 많이 사용했었다. Rejection sampling을 여기서 자세히 다룰 필요는 없기 때문에 간단히 이야기하자면 Rejection sampling에는 두 가지 큰 문제점이 있었는데
- Target distribution이 복잡해지면 복잡해질수록 Approximated distribution이 가지는 샘플 공간이 기하급수적으로 방대해지고 따라서 sampling 성공률이 매우 낮아진다.
- 심지어 매 시행이 독립(independent)이라 어쩌다 재수좋게 옳은 샘플을 선택하더라도 다음번 샘플링은 또 다시 아무런 정보 없이 완전히 blind 상태에서 얻어진다.
MCMC는 특히 굵게 표시한 두번째 문제의 해결에 집중했다. 무한히 많은 수행을 통해 어떤 현상에 대한 실제 확률 분포 p(.)[Target distribution]를 최대한 근사하는 확률 분포 π(.)[Stationary distribution=Stationary States]를 얻되, 매 시행이 독립이라는 가정 대신, 바로 다음에 얻어질 샘플은 바로 직전의 샘플에만 의존(dependent)한다는 개념을 도입하여 샘플링의 효율성을 극대화하는 방식이다.
* 여기서 π(.)는 원주율을 의미하는 π가 아니다. 왜인지 모르겠지만 MCMC를 사용하는 많은 방법들이 구하고자 하는 stationary distribution을 π로 표기한다.
Markov Chain
Markov chain은 Directed probabilistic model로써 특히 다음 발생할 사건은 반드시 그 직전의 사건에 의해서만 영향을 받는다는 가정을 가진 경우이다. 실생활 예시로 날씨 등의 예를 많이 들어 설명하는데 공돌이의 수학노트 영상에서 얘기해준 예시가 더욱 와닿았는데, 예를들어 오늘 먹을 점심을 선택하는데 어제 짜장면을 먹었다면 오늘 점심에 짜장면을 먹으러 가자는 제안은 거절할 가능성이 높아지는 경우가 있겠다. (엄밀히 따지자면 현실에서는 엊그제 먹은 음식도 영향을 주겠지만 그렇게 꼬리를 물기 시작하면 joint distribution을 계산하는 되는 문제가 되는데 이것은 엄청나게 복잡해진다.) MCMC에서 Markov chain은 원하는 실제 분포(Target distribution)을 최대한 근사하는 Stationary distribution π(.)를 얻는 것을 목표로 한다.
Monte Carlo simulation
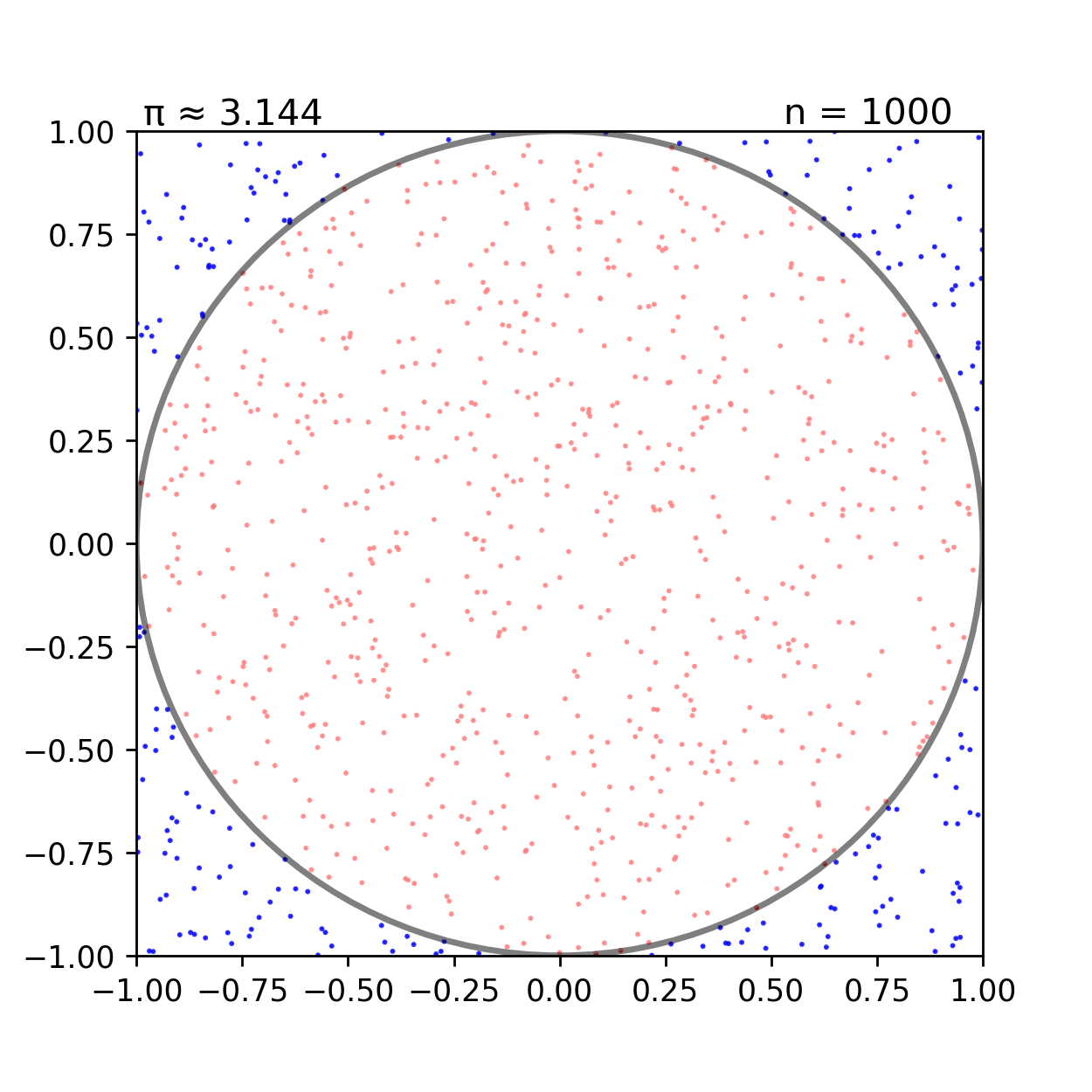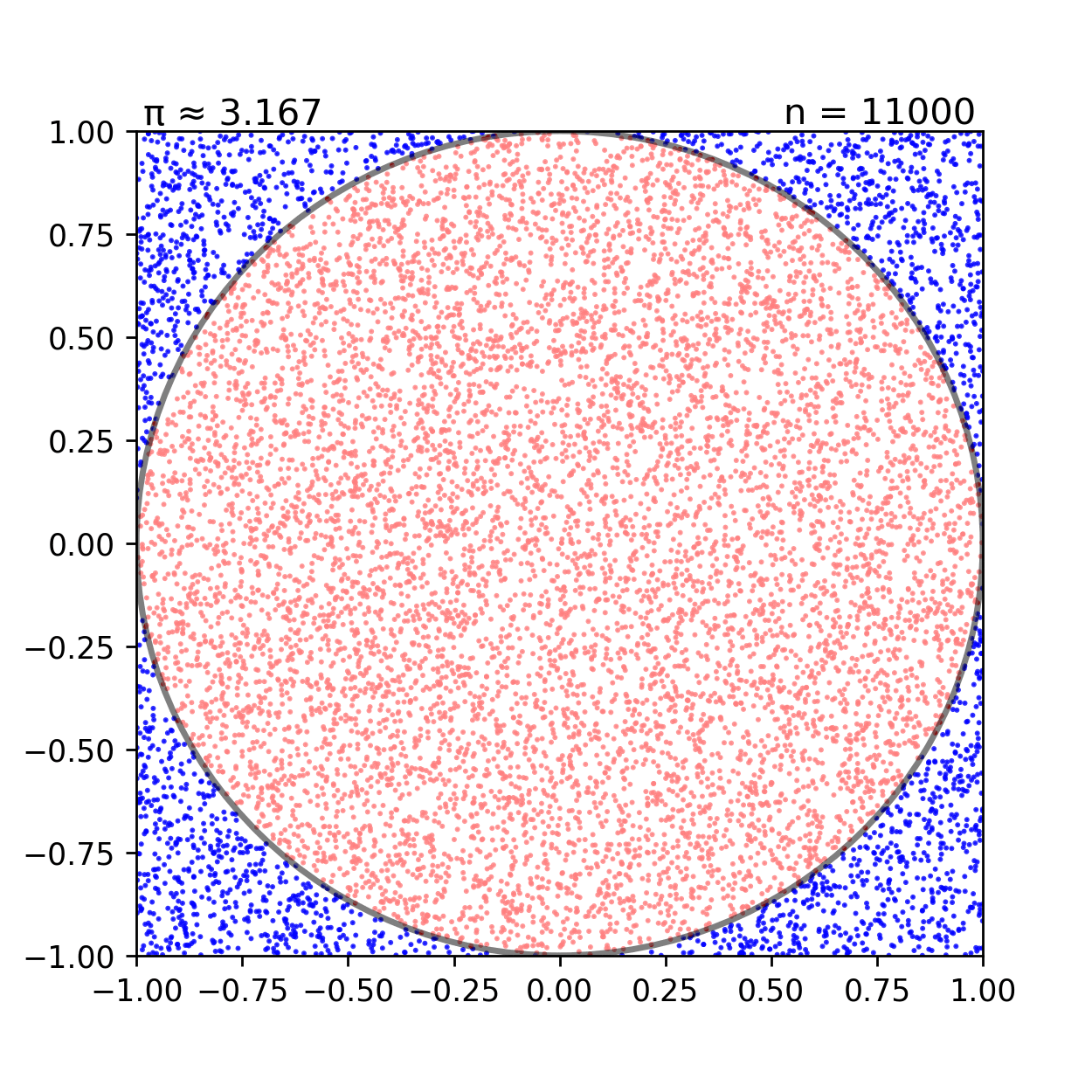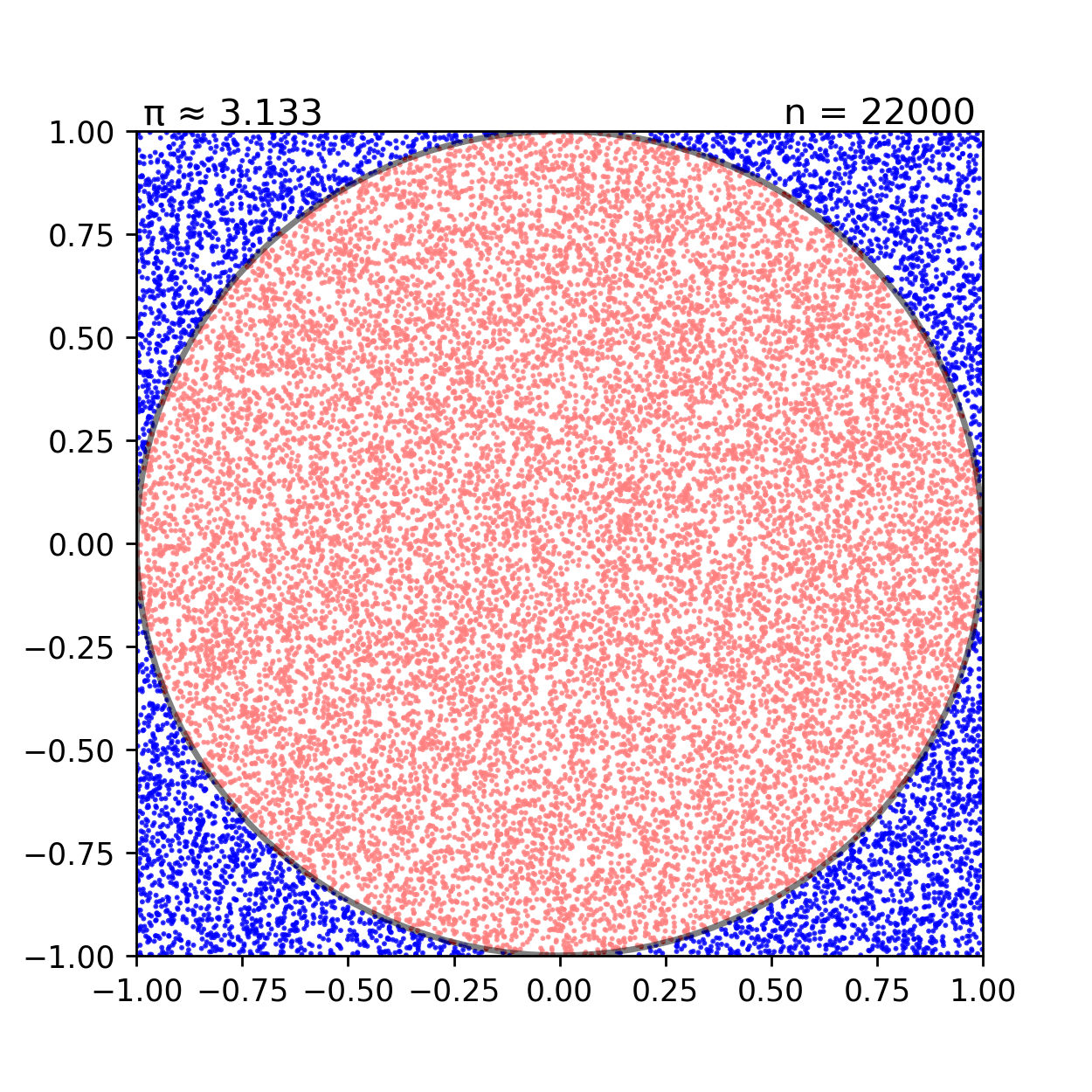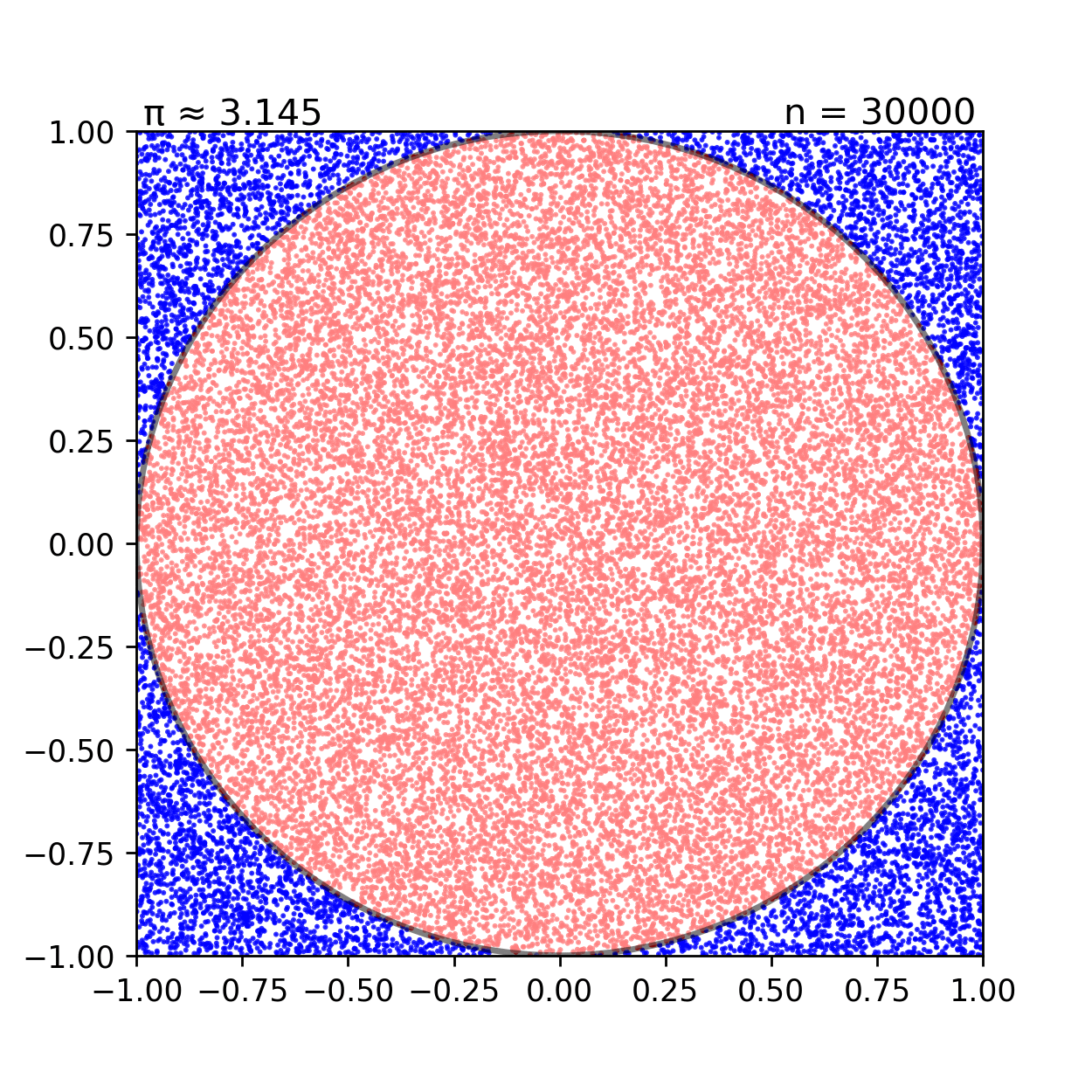
Monte Carlo simulation은 명확히 알 수 없는 수학적인 문제에 대해서 무수하게 많은 sampling을 이용해서 근사치를 구하는 방식을 이야기한다.
왼쪽의 그림을 살펴보자 반지름이 1인 원의 넓이는 어떻게 구하는가? 다음과 같이 무수히 많은 샘플링을 통해 전체 네모 박스에 찍힌 점과 원 내부에 찍힌 점의 비율을 구해보면 실제 원의 넓이 π(3.141592...)에 매우 근사하는 수치가 얻어진다. MCMC에서 Markov chain을 통해 얻어진 Stationary distribution이 실제 분포인 Target distribution을 근사한다면, 이제 Stationary distribution을 이용해 무수히 많은 샘플링을 하는 과정이 바로 Monte Carlo simulation 과정이 된다.
이제 MCMC라는 이름이 붙은 이유는 알았다. 이제 MCMC의 개념에 대해서 알아보자.
MCMC

MCMC를 이해하는데 필요한 중요한 세가지 개념이 있다.
- Transition probability (T(.))
- Stationary State(Stationary distribution) (π(.))
- Detailed balance condition
Transition probability(T)는 임의 state x와 y가 있다고 할때, state x에서 state y로 진행될 확률을 의미하고 T(x|y)로 나타낸다. 다음과 같은 Markov Chain이 있다고 생각하자.
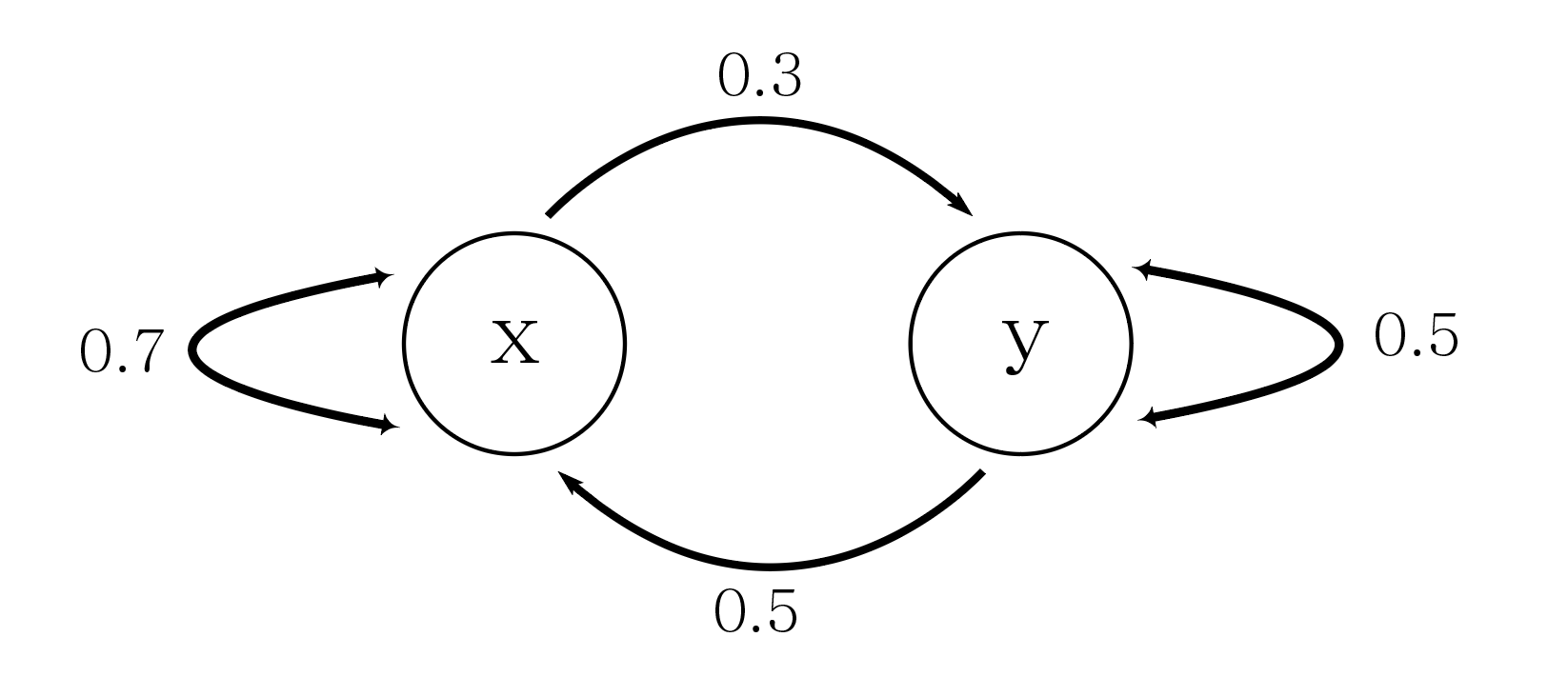
현재 Markov chain에서 transition probability는 다음과 같은 네가지 경우의 수가 존재한다.
- state x 에서 state x로 진행되는 경우 T(x|x) = 0.7
- state x 에서 state y로 진행되는 경우 T(y|x) = 0.3
- state y 에서 state y로 진행되는 경우 T(y|y) = 0.5
- state y 에서 state x로 진행되는 경우 T(x|y) = 0.5
Stationary State(Stationary distribution, π(.))은 Markov chain이 찾고자 하는 실제 Target distribution을 approximation 한다고 생각되는 distribution으로써, Markov chain이 특정 분포로 수렴하기 시작한 후에 나타나는 모든 future states들에 대해서 해당 분포가 계속 유지되는 분포를 의미한다. 이 개념은 말로 설명해서는 명확하게 전달하기 매우 어려워서 이정도로만 정리하자 그러나 MCMC를 이해하기 위해 반드시 이해해야 하는 개념이기 때문에 다음 영상을 시청하기를 강력하게 추천한다. 이후 설명에 사용될 용어들 역시 해당 영상을 보고 이해했다는 가정하에 설명한다.
https://www.youtube.com/watch?v=4sXiCxZDrTU
이제 의문이 생긴다.
- 아니 Markov Chain을 구성하는 states가 한두개일때야 그렇다치는데 실생활 문제를 해결하려면 한두개로 안될텐데?
- 아니 지금 주어진 Markov chain의 Transition probability는 멋대로 설정한 것 아냐? 실생활에선 어떻게 결정하는데?
MCMC는 sampling을 통한 approximation of distribution method라는 큰 가지이다. 실제로 MCMC를 적용하기 위해 Markov chain을 구성하는 transition probability와 stationary distribution을 찾는 방법론은 구체적으로 더 공부해야한다. 가장 대표적인 예시는 Metropolis, Metropolis-Hastings, Gibbs sampling등의 방법이 존재한다. 그러나 이 모든 구체적인 방법론까지 모두 다루기에는 VAEs 이해를 위해 공부를 한다는 나의 목적에서 벗어나는 것 같아서 필요에 따라 추가로 다룰 예정이다.
다만, 모든 방식에서 transition probability와 stationary distribution을 어떻게 design해야 하는지에 대한 공통 기본이 되는 개념인 Detailed balance condition에 대해서는 알고 있어야 한다.
Detailed balance condition
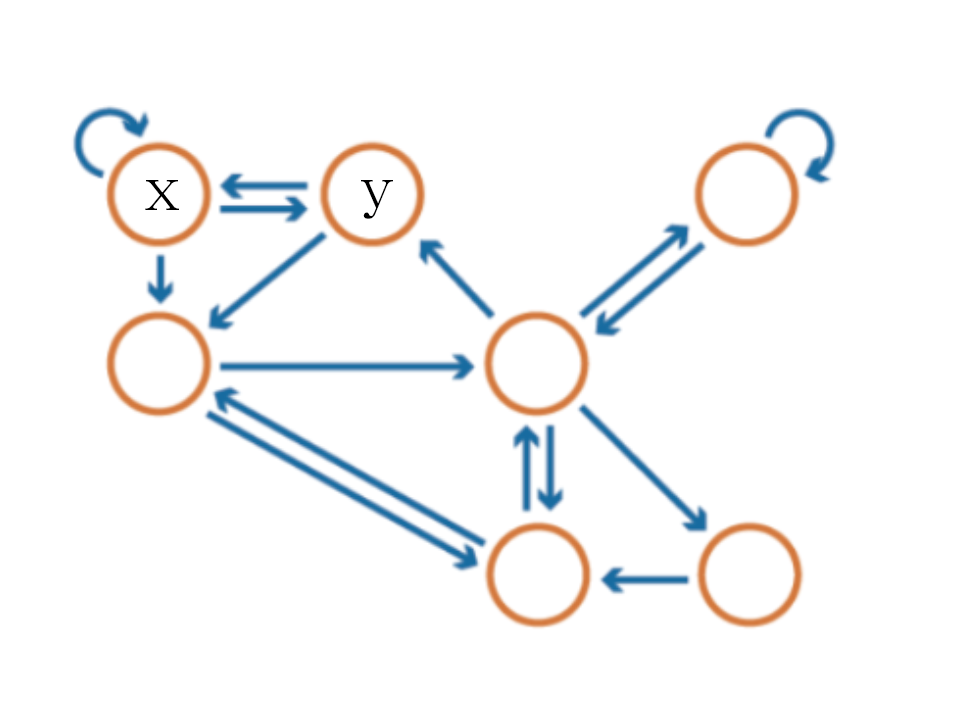
위와 같은 Markov Chain이 있다고 가정하자 임의의 모든 ∀x,y에 대하여 Markov Chain 내부의 두 state x,y를 선택하고 π(x)T(y|x) = π(y)T(x|y)를 만족함을 보이면 해당 Markov chain의 transition probability는 Detailed balance condition을 만족한다고 이야기 한다.
π(x)T(y|x) = π(y)T(x|y)성질을 이용하면 다음과 같은 식을 유도할 수 있다.

(1)식의 가장 왼쪽의 식부터 차근히 설명하면
- π(x)T(y|x) = π(y)T(x|y)라고 했기 때문에 그냥 시그마 내부 식을 바꿔준 것 뿐이고,
- 다음으로 π(y)는 x와 관련 없기 때문에 시그마 내부에서 상수취급하여 밖으로 빼준 것이고,
- 조건부 확률 T(x|y)를 모든 x에 대해서 더해준다는 것은 transition probability의 정의를 생각해보면 'y라는 state가 선택되었을 때, y 주변으로 뻗어나갈 수 있는 모든 state인 x들에 대한 발생 가능성의 총합' 이므로 확률의 정의에 따라 1이 된다.
- 따라서 상수항π(y)만 남게 된다.
그리고 이것은 특정 state 1개에 대한 식이므로 이것을 Stationary vector와 Transition Matrix 형태로 확장하여 생각하면 (2)처럼 식을 바꿔서 표현 할 수 있다. (여기의 p = π로 생각하면 된다.)
여기서 아주 재미있는 식이 나오는데 pT = p라는 식, 어디서 많이 본 형태 아닌가? 고유값과 고유 벡터를 구하는 행렬 방정식에서 자주 보던 Ax = bx 형태이다. 다시말하면 Matrix T에 대해서 EigenValue가 1인 EigenVector p를 구하는 문제로 볼 수 있다.
'Background > Math' 카테고리의 다른 글
- Total
- Today
- Yesterday
- 최대우도추정
- 나노바디
- marginal likelihood
- elementry matrix
- 3B1B따라잡기
- 이왜안
- dataloader
- manim
- manimtutorial
- 항원항체결합예측모델
- antigen antibody interaction prediction
- 오일석기계학습
- Manimlibrary
- 선형대수
- 베이즈정리
- 백준
- Matrix algebra
- MorganCircularfingerprint
- nanobody
- 논문리뷰
- MatrixAlgebra
- 3b1b
- 기계학습
- manim library
- ai신약개발
- MLE
- eigenvalue
- 인공지능
- eigenvector
- 파이썬
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
