understanding diffusion models: a unified perspective "equation 43~45" 유도과정

Diffusion 논문을 공부해본 사람들이면 한번쯤은 봤을 논문이다.

다른거 다 제쳐두고 다음 43~45 equation을 이해하는데 정말이지 2주는 걸린 것 같다.

Equation 43 ~ 45

 

1. Expectation 아래 q(-) 분포가 왜 갑자기 축소되는가?

Expectation 아래 q분포가 왜 축소되는가?

: 이것은 그나마 이해하기 쉽다. 우선 아래 수식을 노트에 한번 따라써보면서 이해해보자.

https://zhuanlan.zhihu.com/p/638240916

 

다시말하면 E__{x~q(x),y~p(y),z~h(z)}[f(x)] 같은 식이 있다고 할 때, y나 z는 Expectation내부 함수 f(x)에 전혀 영향을 주지 않는 변수이므로 아예 식에서 제외해버려도 상관 없다. 정말 직관적으로 생각하자면 Expectation [...] 에 들어가지 않는 변수들은 모두 제거해도 된다는 의미이다.

따라서 각 Expectation 내부에 있는 함수에 포함되지 않는 변수들을 모두 제거한 뒤 축약하면 equation 43 -> 44는 해결된다.

 

2. Equation 44에서 45로 갈때, Consistency term의 유도

consistency term의 유도방식을 모르겠다.

Equation(44)에서 Equation(45)에서 특히 Consistency term으로의 유도가 이해가 안가서 정말 몇날 며칠을 머리를 쥐어잡고 이해하기 위해서 싸웠다. 결과적으로 맞는지는 확실하진 않지만 내가 이해한 방식을 나름대로 설명해보려 한다.

이해를 위해서는 베이즈 룰, Joint probability, 확률의 Chain Rule, Markov property, Expectation의 정의로부터 integral 표현식으로 나타내는 방법, KL Divergence를 알고있어야 한다. 

먼저 Equation(44)의 다음 Expectation부터 살펴보자.

식1.

베이즈 룰에 의해 q는 다음과 같이 나타낼 수 있다.

식2.

분자는 joint probability이므로 순서는 영향이 없다. 따라서

식3.

식3의 우항을 베이즈룰을 이용해서 정리해보면

식4. Baye's Rule과 Chain rule 이용

최종적으로 맨 아래의 식5 으로 정리할 수 있다.

식5.

여기서 DDPM논문의 Markov property를 생각해보면 forward process의 x_t는 오직 x_t-1의 영향만 받는다. 따라서 식5에서 다음 condition들은 변수에 영향을 주지 않는 condition이기 때문에 식6에 나타낸 빨간 부분은 제거하고 식7처럼 나타내도 무방하다.

논문에 그렇다고 되어있다.

식6.

그러면 다음 식7로 정리가 되는데 

식7.

이를 식2 또는 식3에 대입하여 정리하면 식8이 완성된다.

식8.

 

2-1. 이제 이를 이용해서 Consistency term을 유도해보자

여기서부터는 Expectation이나 Integral형태로부터 KLD term을 유도하는 방법정도는 알고있다는 가정하에 설명합니다.

식9. log 성질을 이용해 negative Expectation으로 바꾸고 분자 분모 순서바꿈

식10. Expectation의 정의에 따라 Integral로 나타냄

식11. Integral 내부 식의 순서를 정리하여 KLD term으로 바꿀 수 있는 항을 만듬

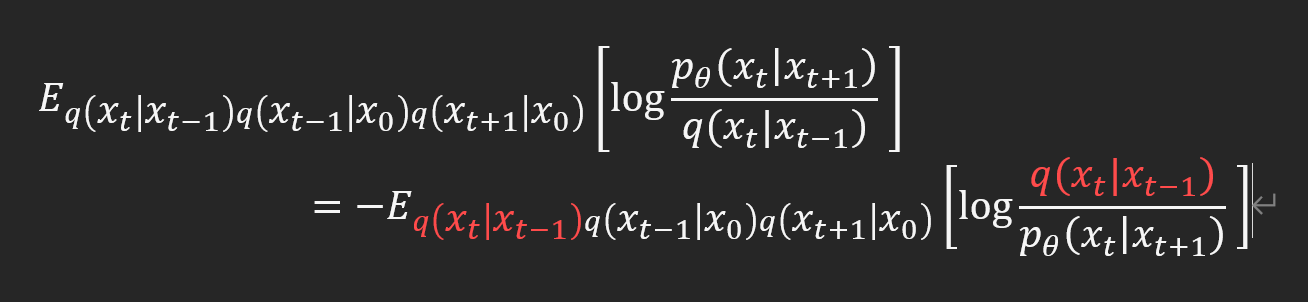
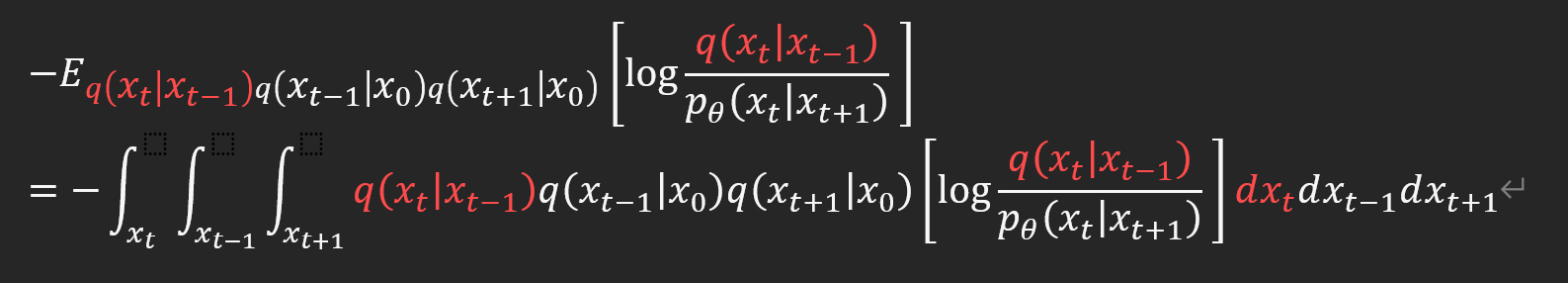
식 11까지의 유도과정은 Expectation과 Integral에서 KLD term의 유도와 Expectation의 정의로부터 integral형태로 바꾸는 방법 두가지를 알고 있다면 손으로 직접 해보면 이해할 수 있다.

또한 KLD term을 integral 또는 expectation으로부터 유도하는 방법을 알고 있다면 식 11에서 파란 네모박스 부분의 식이 KLD term으로 바꿔 쓸 수 있다는 것도 알 수 있다. 이를 이용하면 식 12로 완성할 수 있다.

식12.

여기서 다시 Expectation의 정의를 이용해서 Integral을 Expectation 형태로 바꿔주면

식13. 최종 얻어진 consistency term

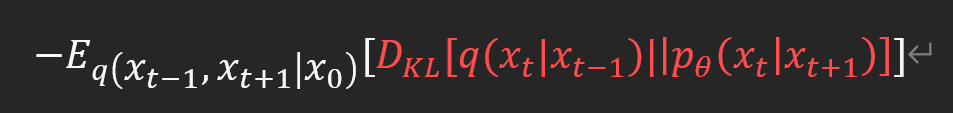
이렇게 equation44에서 45로 넘어가는 방법도 확인할 수 있었다.

 

수식 유도 과정에서 약간의 뇌피셜이 들어갔다. 그치만 어차피 AI분야는 약간의 뇌피셜은 깔아놓고 가는건 대부분 똑같다고 본다. 바라건대 누군가 이 글을 보다가 명확한 오류가 있다면 제발 사람 살린다는 마음으로 그냥 뒤로가기 누르지 마시고 제발 지적해주시길 바란다. 해답까지 알려달라고는 바라지 않습니다. 제가 찾아서 공부할 수 있도록 그냥 틀린부분을 틀렸다고 말씀만이라도 정중히 부탁드립니다.