티스토리 뷰
Background/Math
선형대수 Matrix algebra 용어 및 기초이론 정리/모음 (3) - Partitioned Matrix / Matrix Factorization
벼랑끝과학자 2023. 5. 29. 03:08Vector는 소문자 bold체로 나타냅니다(v) 소문자이면서 bold체가 아닌 경우(a)는 상수를 나타냅니다.
제곱이나 아래첨자를 업데이트 하지만 티스토리 블로그 특성상 작성이 불편하기 때문에 오타가 있을 수 있습니다.
multiple은 기호(x)로, 내적(dot product)은 기호 ()로 표시합니다.
구체적인 내용에 대한 전달이 아니라 기초적인 선형대수학의 정리를 모아놓는 포스팅입니다.
작성되는 포스팅은 모두 인프런 - 타블렛깍는노인 조범희님의 강의를 바탕으로 작성했습니다.
(강의 정말 좋습니다. 혹시 생각있으시면 돈 안아깝습니다. 한번 해보세요)
2023.05.25 - [Background/Math] - 선형대수학 용어 및 기초 이론 정리/모음
2023.05.26 - [Background/Math] - 선형대수 Matrix algebra 용어 및 기초이론 정리/모음 (1) - 전치행렬과 역행렬
2023.05.27 - [Background/Math] - 선형대수 Matrix algebra 용어 및 기초이론 정리/모음 (2) - Elementry matrix
- Partitioned Matrix : Matrix의 부분을 나눠 sub matrix로 표현 (= block matrix)
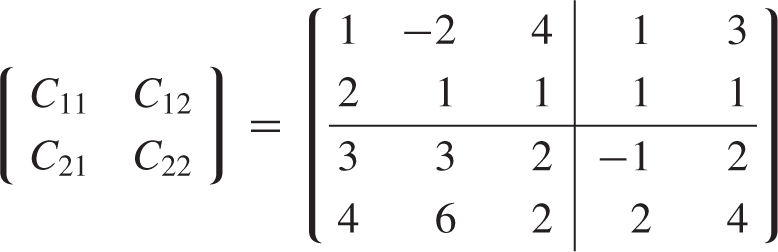
- Partitioned Matrix A, B를 Multiplication할때는 A의 column을 나눈 형태와 B의 row를 나눈 형태가 같아야한다.
- A의 row와 B의 column을 어떻게 나누었는지는 상관 없다.
- Partitoned Matrix Multiplication이 가능한 형태로 partion된 것을 Conformable Matrix라고 한다.
정리10.
Matrix A가 m*n이고 B가 n*p라고 하자. 이때 AB는 다음과 같이 나타낼 수 있다
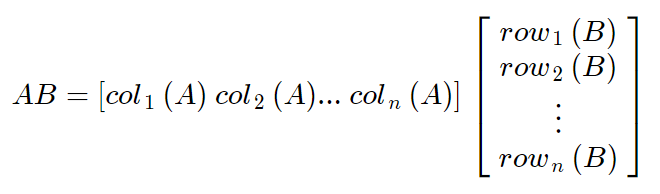
- 또는 AB = [Ab1 Ab2 ... Abp]로 나타낼 수도 있다. (bn은 Matrix B의 n번째 column)
- Matrix Factorization : 어떤 Matrix를 다른 2개 이상의 Matrix의 곱으로 나타낸 것 ex) A = BC
- LU Factorization : 특히 어떤 Matrix를 다음과 같은 형태로 나타냈을 때 이를 LU Factorization이라고 한다.
-
- Unit Lower Triangular Matrix(L)
- Echelone Form(U)
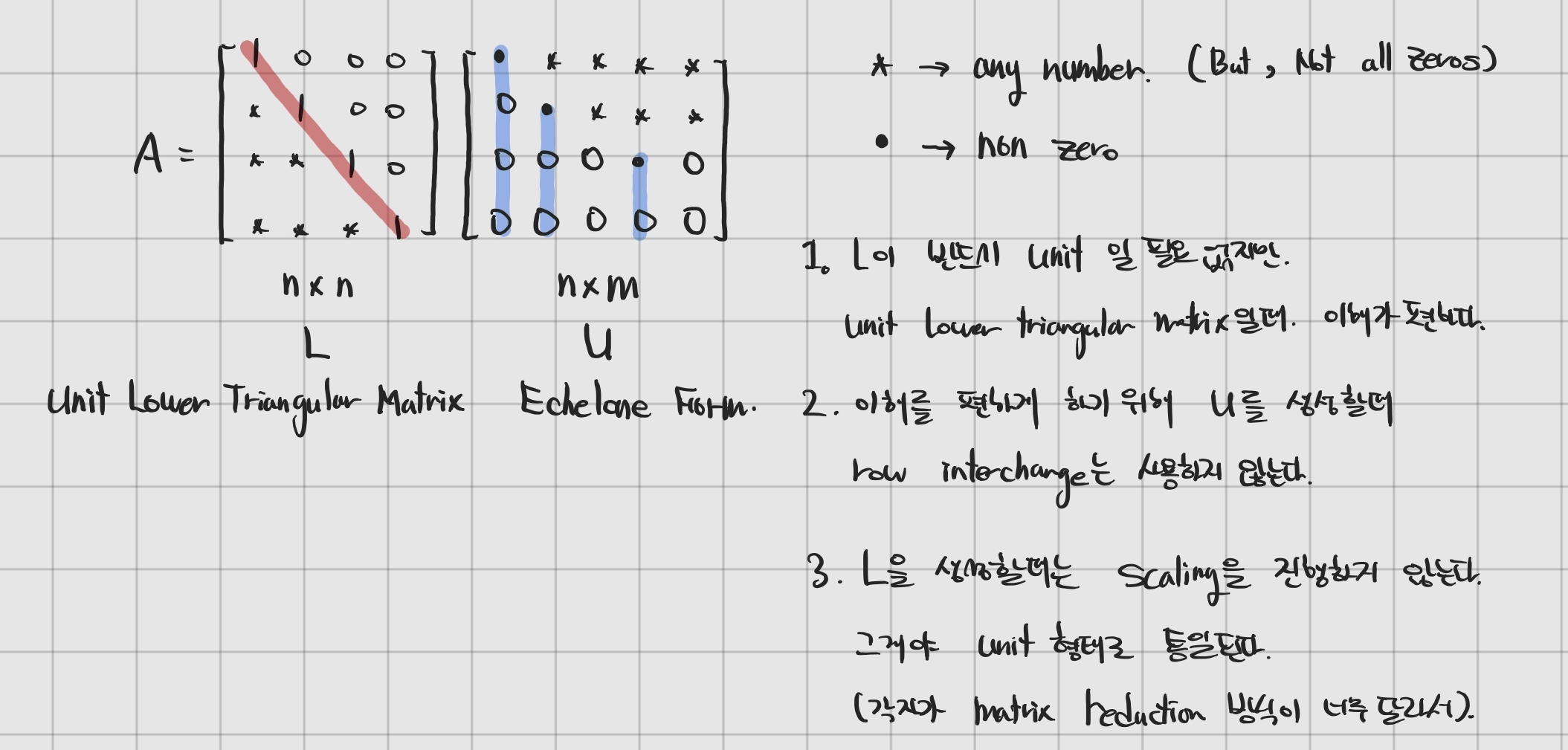
- LU Factorization은 왜 유용한가?
- A = LU라고 하자, 이때 Ax = b를 풀때 다음과 같이 사용 가능하다.
- Ax = b에서 A를 LU로 나타내면 LUx = b이다.
- Ux = y로 치환하면 Ly = b이다.
- 따라서 Ax = b문제를 Ly = b와 Ux = y 문제로 치환하여 풀 수 있다.
- 자세한 이유까지는 언급하지 않겠지만, x에 A-1b를 대입해서 풀때보다 LU Factorization으로 문제를 풀 때 computational cost가 적어져 효율적인 경우가 많다.
- 또 보통 컴퓨터공학적으로 문제를 해결할 때, Matrix A가 상당히 sparse한 경우가 많은데, 아이러니하게도 많은 경우에 A-1는 굉장히 dense하다. 반면 LU Matrix는 A처럼 sparse한 경우가 많다. 따라서, 컴퓨터 계산시의 memory도 상당부분 절약이 가능하다.
- A = LU라고 하자, 이때 Ax = b를 풀때 다음과 같이 사용 가능하다.

- 그럼 어떻게 L과 U를 구하는가? LU를 구하는 algorithm을 알아보자
- Row operation은 replacement만 사용한다는 것을 전제로 한다.
- Elementry matrix에 대한 선행 지식이 반드시 필요하다. (이전 Elementry matrix 포스팅 참고)
- Row operation은 matrix A에 Elementry matrix를 곱하는 형태였다.
- (Ep...E1)A = U (Echelone form) (=Forward phase)
- 이때 replacement만 사용하기로 하였기 때문에 Elementry matrix는 반드시 unit triangular elementry matrix이다.
- 따라서 Elementry matrix를 몇번을 곱하던지 (Ep...E1)은 반드시 L형태를 만족한다.
- Unit Lower triangular elementry matrix특성상 그 역함수(Ep...E1)-1 역시 반드시 L형태를 만족한다.
- 따라서 L = (Ep...E1)-1로 치환하면 A = LU 형태가 된다.
- 이때 항등항렬 I를 곱하는 것은 결과에 영향이 없으므로 L = (Ep...E1)-1I라고하자
- 역함수의 성질에 의해 L = (E1-1...Ep-1)I가 된다.
- 한마디로 정리하면, 어떤 임의의 matrix A를 U(Echelone Form)을 만들기 위해 수행한 Elementry matrix들의 [역함수!]를 항등행렬 I에 역순(또는 정순)으로 수행하면 L이 만들어진다.


- 지금까지의 내용을 이해했다면 아래 예시를 이해할 수 있어야한다.

- 이번에는 U를 만들기 위해서 Interchange가 반드시 필요한 경우를 다뤄보자
- 글로 설명하기가 너무 어려워서 동영상으로 대체함
'Background > Math' 카테고리의 다른 글
| 선형대수 Matrix algebra 용어 및 기초이론 정리/모음 (5) - Coordinate system / Dimension and Rank (0) | 2023.05.30 |
|---|---|
| 선형대수 Matrix algebra 용어 및 기초이론 정리/모음 (4) - Subspaces (0) | 2023.05.29 |
| 선형대수 Matrix algebra 용어 및 기초이론 정리/모음 (2) - Elementry matrix (0) | 2023.05.27 |
| 선형대수 Matrix algebra 용어 및 기초이론 정리/모음 (1) - 전치행렬과 역행렬 (0) | 2023.05.26 |
| 선형대수학 Linear Algebra 용어 및 기초 이론 정리/모음 (0) | 2023.05.25 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- 인공지능
- Manimlibrary
- MLE
- 백준
- marginal likelihood
- elementry matrix
- 최대우도추정
- antigen antibody interaction prediction
- 선형대수
- 3B1B따라잡기
- eigenvector
- MorganCircularfingerprint
- 논문리뷰
- 항원항체결합예측모델
- manim
- MatrixAlgebra
- manimtutorial
- ai신약개발
- 오일석기계학습
- 파이썬
- nanobody
- 나노바디
- eigenvalue
- 베이즈정리
- dataloader
- 이왜안
- 3b1b
- Matrix algebra
- 기계학습
- manim library
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함
