티스토리 뷰
Vector는 소문자 bold체로 나타냅니다(v) 소문자이면서 bold체가 아닌 경우(a)는 상수를 나타냅니다.
제곱이나 아래첨자를 업데이트 하지만 티스토리 블로그 특성상 작성이 불편하기 때문에 오타가 있을 수 있습니다.
구체적인 내용에 대한 전달이 아니라 기초적인 선형대수학의 정리를 모아놓는 포스팅입니다.
작성되는 포스팅은 모두 인프런 - 타블렛깍는노인 조범희님의 강의를 바탕으로 작성했습니다.
2023.05.25 - [Background/Math] - 선형대수학 Linear Algebra 용어 및 기초 이론 정리/모음
2023.05.26 - [Background/Math] - 선형대수 Matrix algebra 용어 및 기초이론 정리/모음 (1) - 전치행렬과 역행렬
2023.05.27 - [Background/Math] - 선형대수 Matrix algebra 용어 및 기초이론 정리/모음 (2) - Elementry matrix
- Subspace : 다음 세 조건을 만족하는 모든 set H를 Rn space의 subspace라고 한다.
- Zero vector 가 H내부에 존재한다.
- H 내부의 임의 벡터 u와 v에 대해 u+v도 set H에 존재한다.
- H 내부의 임의 벡터 u에 대해 cu도 set H에 존재한다.
- 2와 3을 덧셈과 scalar 곱에 대해 닫혀있다(closed)고 표현한다.

- Column space : 어떤 matrix A가 주어졌을 때, matrix A의 모든 column들의 span을 column space라고 한다.
- A = [a1 ... an]일때 column space = span{a1 ... an}
- 다음 세가지 문장은 같은 의미이다.
- 특정 vector b가 A의 column space에 존재하는가?
- b가 span{a1 ... an}에 존재하는가?
- Ax = b가 consistent한가?
- Column space A의 Basis는 Matrix A의 pivot column들이다.
- Null space : matrix A의 null space는 Transformation A에 의해 zero vector로 이동되는 모든 x들의 집합이다.
- 다시말해 Homogeneous Equation Ax = 0의 solution set을 Null A라고 한다.
- vector u가 Null A에 존재하는가? <=> Au = 0가 consistent한가?
정리11.
m * n Matrix A가 있다고 하자, 이때 Null A는 Rn의 subspace이다.
- zero vector가 Subspace Null A에 존재하는가?
- A0 = 0 이므로 조건을 만족한다.
- 임의 벡터 u와 v에 대해 u+v도 subspace에 존재하는가?
- Au = 0이고 Av = 0일때 A(u+v) = 0이므로 조건을 만족한다.
- 임의 벡터 u에 대해 cu도 subspace에 존재하는가?
- Au = 0이고, A(cu) = c0 = 0 이므로 조건을 만족한다.
따라서 Null A는 Rn의 subspace이다.
- Null space는 implicitly defined 되었다고 말한다.
- Column space는 explicitly defined 되었다고 말한다.
- Basis for a subspace : Rn space의 subspace H를 span하는 linearly independent 한 set을 Basis라고 한다.
- 사실 Rn space 자신도 subspace조건에 의해 Rn space의 subspace이다.
- 따라서 그냥 Rn space의 Basis라고 이해해도 된다.
- 특정 subspace에 대한 Basis는 유일무이하지 않다. 사람마다 다양하게 표현할 수 있다.
- 그러나 Standard basis는 유일하다.
Basis에 대한 설명은 동영상으로 대체합니다.
06:38 linear combination이 아니라 linearly independent를 이야기하려던게 꼬였습니다 😂
정리12.
Matrix A의 pivot column들은 Column space A의 Basis이다.
- 즉 Matrix A의 pivot column들은 Column space A를 span한다.
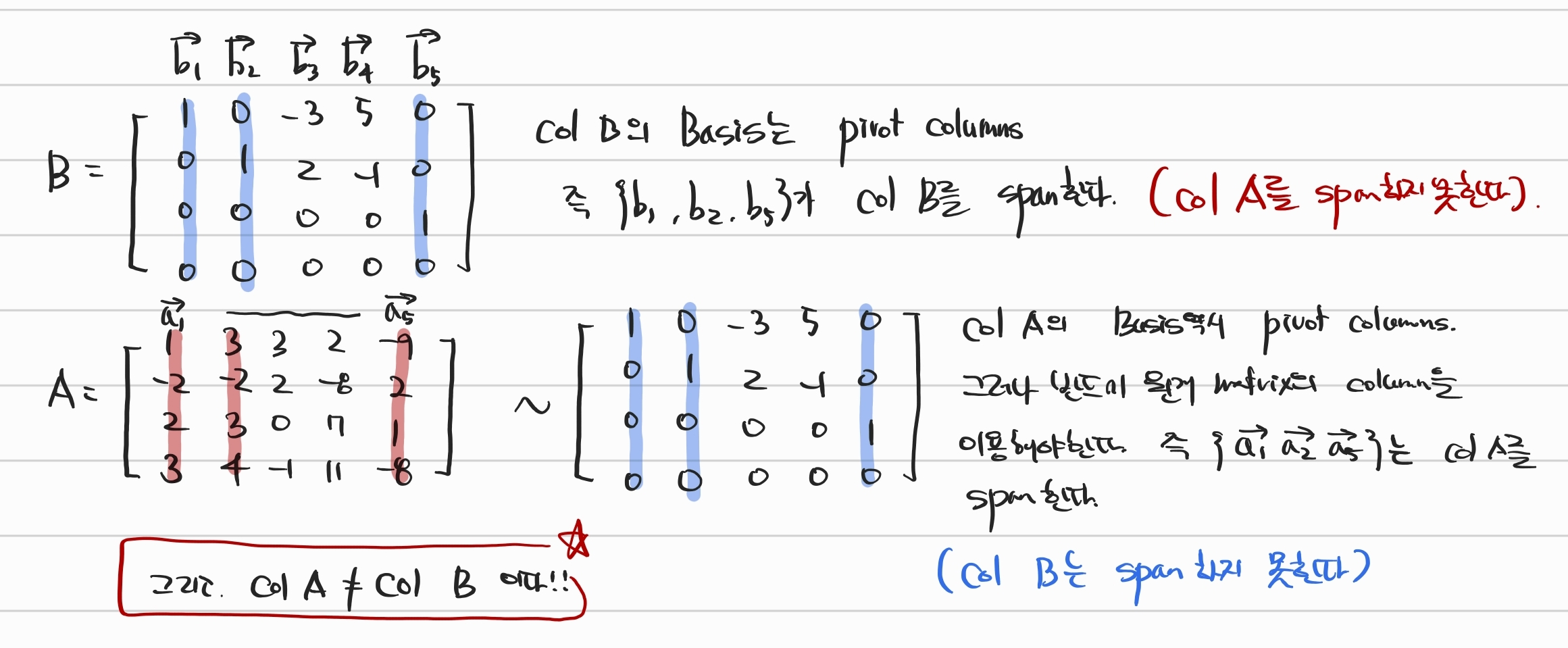
- Matrix A를 어떻게 row operation 하던지, Matrix A와 Row operated Matrix의 pivot columns position은 항상 같다.
- 그러나 Operated Matrix의 column space는 원래 Matrix A의 column space와 전혀 다른 공간이다.
- 따라서 정리12에서 이야기한 Column space의 basis도 전혀 달라진다.
'Background > Math' 카테고리의 다른 글
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- 최대우도추정
- 이왜안
- 백준
- 베이즈정리
- MatrixAlgebra
- 오일석기계학습
- dataloader
- Manimlibrary
- 3B1B따라잡기
- eigenvector
- 선형대수
- manimtutorial
- 파이썬
- 나노바디
- elementry matrix
- manim
- 논문리뷰
- 3b1b
- marginal likelihood
- MorganCircularfingerprint
- 인공지능
- 항원항체결합예측모델
- ai신약개발
- nanobody
- antigen antibody interaction prediction
- Matrix algebra
- eigenvalue
- 기계학습
- manim library
- MLE
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함
